Post Syndicated from Lejla Batina (Guest author) original https://blog.cloudflare.com/kyber-isnt-broken/


News coverage of a recent paper caused a bit of a stir with this headline: “AI Helps Crack NIST-Recommended Post-Quantum Encryption Algorithm”. The news article claimed that Kyber, the encryption algorithm in question, which we have deployed world-wide, had been “broken.” Even more dramatically, the news article claimed that “the revolutionary aspect of the research was to apply deep learning analysis to side-channel differential analysis”, which seems aimed to scare the reader into wondering what will Artificial Intelligence (AI) break next?
Reporting on the paper has been wildly inaccurate: Kyber is not broken and AI has been used for more than a decade now to aid side-channel attacks. To be crystal clear: our concern is with the news reporting around the paper, not the quality of the paper itself. In this blog post, we will explain how AI is actually helpful in cryptanalysis and dive into the paper by Dubrova, Ngo, and Gärtner (DNG), that has been misrepresented by the news coverage. We’re honored to have Prof. Dr. Lejla Batina and Dr. Stjepan Picek, world-renowned experts in the field of applying AI to side-channel attacks, join us on this blog.
We start with some background, first on side-channel attacks and then on Kyber, before we dive into the paper.
Breaking cryptography
When one thinks of breaking cryptography, one imagines a room full of mathematicians puzzling over minute patterns in intercepted messages, aided by giant computers, until they figure out the key. Famously in World War II, the Nazis’ Enigma cipher machine code was completely broken in this way, allowing the Allied forces to read along with their communications.

It’s exceedingly rare for modern established cryptography to get broken head-on in this way. The last catastrophically broken cipher was RC4, designed in 1987, while AES, designed in 1998, stands proud with barely a scratch. The last big break of a cryptographic hash was on SHA-1, designed in 1995, while SHA-2, published in 2001, remains untouched in practice.
So what to do if you can’t break the cryptography head-on? Well, you get clever.
Side-channel attacks
Can you guess the pin code for this gate?

You can clearly see that some of the keys are more worn than the others, suggesting heavy use. This observation gives us some insight into the correct pin, namely the digits. But the correct order is not immediately clear. It might be 1580, 8510, or even 115085, but it’s a lot easier than trying every possible pin code. This is an example of a side-channel attack. Using the security feature (entering the PIN) had some unintended consequences (abrading the paint), which leaks information.
There are many different types of side channels, and which one you should worry about depends on the context. For instance, the sounds your keyboard makes as you type leaks what you write, but you should not worry about that if no one is listening in.
Remote timing side channel
When writing cryptography in software, one of the best known side channels is the time it takes for an algorithm to run. For example, let’s take the classic example of creating an RSA signature. Grossly simplified, to sign a message m with private key d, we compute the signature s as md (mod n). Computing the exponent of a big number is hard, but luckily, because we’re doing modular arithmetic, there is the square-and-multiply trick. Here is a naive implementation in pseudocode:

The algorithm loops over the bits of the secret key, and does a multiply step if the current bit is a 1. Clearly, the runtime depends on the secret key. Not great, but if the attacker can only time the full run, then they only learn the number of 1s in the secret key. The typical catastrophic timing attack against RSA instead is hidden behind the “mod n”. In a naive implementation this modular reduction is slower if the number being reduced is larger or equal n. This allows an attacker to send specially crafted messages to tease out the secret key bit-by-bit and similar attacks are surprisingly practical.
Because of this, the mantra is: cryptography should run in “constant time”. This means that the runtime does not depend on any secret information. In our example, to remove the first timing issue, one would replace the if-statement with something equivalent to:
s = ((s * powerOfM) mod n) * bit(s, i) + s * (1 - bit(s, i))
This ensures that the multiplication is always done. Similar countermeasures prevent practically all remote timing attacks.
Power side-channel
The story is quite different for power side-channel attacks. Again, the classic example is RSA signatures. If we hook up an oscilloscope to a smartcard that uses the naive algorithm from before, and measure the power usage while it signs, we can read off the private key by eye:
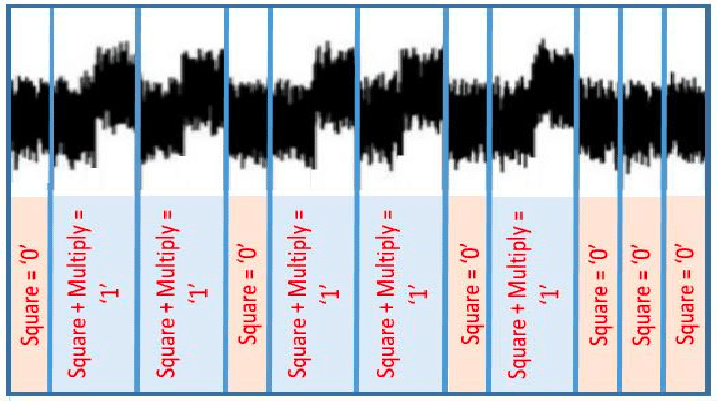
Even if we use a constant-time implementation, there are still minute changes in power usage that can be detected. The underlying issue is that hardware gates that switch use more power than those that don’t. For instance, computing 127 + 64 takes more energy than 64 + 64.
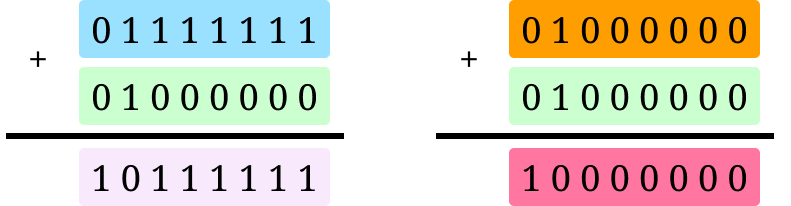
Masking
A common countermeasure against power side-channel leakage is masking. This means that before using the secret information, it is split randomly into shares. Then, the brunt of the computation is done on the shares, which are finally recombined.
In the case of RSA, before creating a new signature, one can generate a random r and compute md+r (mod n) and mr (mod n) separately. From these, the final signature md (mod n) can be computed with some extra care.
Masking is not a perfect defense. The parts where shares are created or recombined into the final value are especially vulnerable. It does make it harder for the attacker: they will need to collect more power traces to cut through the noise. In our example we used two shares, but we could bump that up even higher. There is a trade-off between power side-channel resistance and implementation cost.
One of the challenging parts in the field is to estimate how much secret information is actually leaked through the traces, and how to extract it. Here machine learning enters the picture.
Machine learning: extracting the key from the traces
Machine learning, of which deep learning is a part, represents the capability of a system to acquire its knowledge by extracting patterns from data — in this case, the secrets from the power traces. Machine learning algorithms can be divided into several categories based on their learning style. The most popular machine learning algorithms in side-channel attacks follow the supervised learning approach. In supervised learning, there are two phases: 1) training, where a machine learning model is trained based on known labeled examples (e.g., side-channel measurements where we know the key) and 2) testing, where, based on the trained model and additional side-channel measurements (now, with an unknown key), the attacker guesses the secret key. A common depiction of such attacks is given in the figure below.
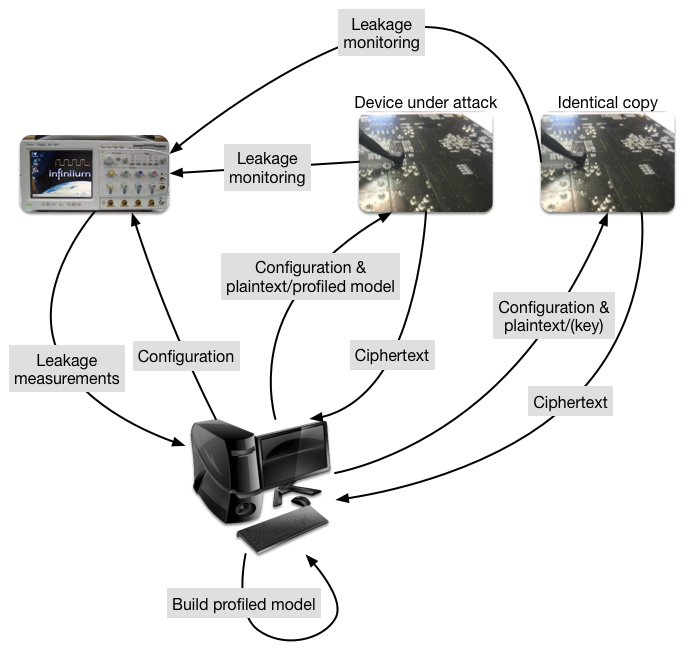
While the threat model may sound counterintuitive, it is actually not difficult to imagine that the attacker will have access (and control) of a device similar to the one being attacked.
In side-channel analysis, the attacks following those two phases (training and testing) are called profiling attacks.
Profiling attacks are not new. The first such attack, called the template attack, appeared in 2002. Diverse machine learning techniques have been used since around 2010, all reporting good results and the ability to break various targets. The big breakthrough came in 2016, when the side-channel community started using deep learning. It greatly increased the effectiveness of power side-channel attacks both against symmetric-key and public-key cryptography, even if the targets were protected with, for instance, masking or some other countermeasures. To be clear: it doesn’t magically figure out the key, but it gets much better at extracting the leaked bits from a smaller number of power traces.
While machine learning-based side-channel attacks are powerful, they have limitations. Carefully implemented countermeasures make the attacks more difficult to conduct. Finding a good machine learning model that can break a target can be far from trivial: this phase, commonly called tuning, can last weeks on powerful clusters.
What will the future bring for machine learning/AI in side-channel analysis? Counter intuitively, we would like to see more powerful and easy to use attacks. You’d think that would make us worse off, but to the contrary it will allow us to better estimate how much actual information is leaked by a device. We also hope that we will be able to better understand why certain attacks work (or not), so that more cost-effective countermeasures can be developed. As such, the future for AI in side-channel analysis is bright especially for security evaluators, but we are still far from being able to break most of the targets in real-world applications.
Kyber
Kyber is a post-quantum (PQ) key encapsulation method (KEM). After a six-year worldwide competition, the National Institute of Standards and Technology (NIST) selected Kyber as the post-quantum key agreement they will standardize. The goal of a key agreement is for two parties that haven’t talked to each other before to agree securely on a shared key they can use for symmetric encryption (such as Chacha20Poly1305). As a KEM, it works slightly different with different terminology than a traditional Diffie–Hellman key agreement (such as X25519):
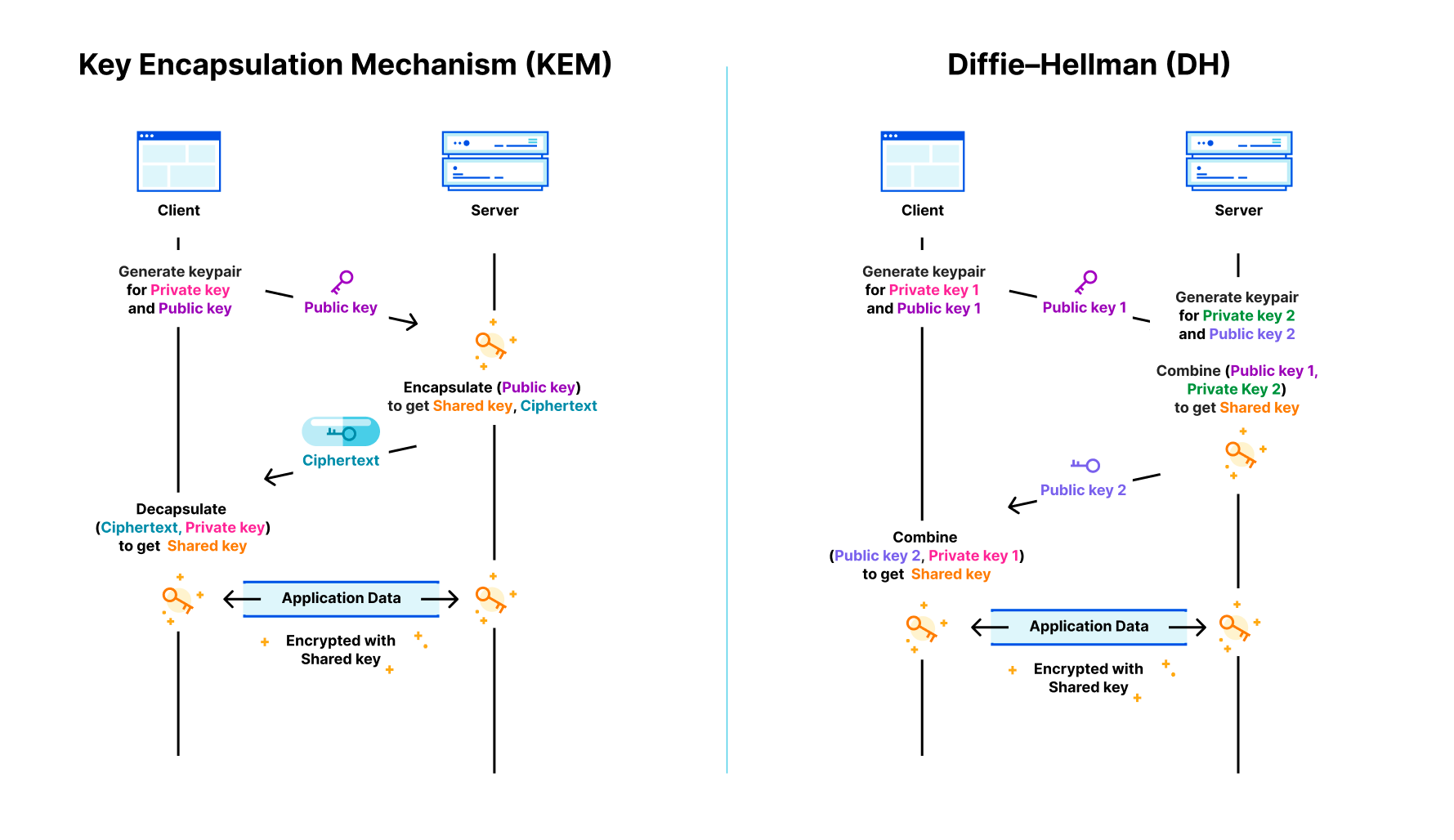
When connecting to a website the client first generates a new ephemeral keypair that consists of a private and public key. It sends the public key to the server. The server then encapsulates a shared key with that public key, which gives it a random shared key, which it keeps, and a ciphertext (in which the shared key is hidden), which the server returns to the client. The client can then use its private key to decapsulate the shared key from the ciphertext. Now the server and client can communicate with each other using the shared key.
Key agreement is particularly important to make secure against attacks of quantum computers. The reason is that an attacker can store traffic today, and crack the key agreement in the future, revealing the shared key and all communication encrypted with it afterwards. That is why we have already deployed support for Kyber across our network.
The DNG paper
With all the background under our belt, we’re ready to take a look at the DNG paper. The authors perform a power side-channel attack on their own masked implementation of Kyber with six shares.
Point of attack
They attack the decapsulation step. In the decapsulation step, after the shared key is extracted, it’s encapsulated again, and compared against the original ciphertext to detect tampering. For this re-encryption step, the precursor of the shared key—let’s call it the secret—is encoded bit-by-bit into a polynomial. To be precise, the 256-bit secret needs to be converted to a polynomial with 256 coefficients modulo q=3329, where the ith coefficient is (q+1)/2 if the ith bth is 1 and zero otherwise.
This function sounds simple enough, but creating a masked version is tricky. The rub is that the natural way to create shares of the secret is to have shares that xor together to be the secret, and that the natural way to share polynomials is to have shares that add together to get to the intended polynomial.
This is the two-shares implementation of the conversion that the DNG paper attacks:

The code loops over the bits of the two shares. For each bit, it creates a mask, that’s 0xffff if the bit was 1 and 0 otherwise. Then this mask is used to add (q+1)/2 to the polynomial share if appropriate. Processing a 1 will use a bit more power. It doesn’t take an AI to figure out that this will be a leaky function. In fact, this pattern was pointed out to be weak back in 2016, and explicitly mentioned to be a risk for masked Kyber in 2020. Apropos, one way to mitigate this, is to process multiple bits at once — for the state of the art, tune into April 2023’s NIST PQC seminar. For the moment, let’s allow the paper its weak target.
The authors do not claim any fundamentally new attack here. Instead, they improve the effectiveness of the attack in two ways: the way they train the neural network, and how to use multiple traces more effectively by changing the ciphertext sent. So, what did they achieve?
Effectiveness

To test the attack, they use a Chipwhisperer-lite board, which has a Cortex M4 CPU, which they downclock to 24Mhz. Power usage is sampled at 24Mhz, with high 10-bit precision.
To train the neural networks, 150,000 power traces are collected for decapsulation of different ciphertexts (with known shared key) for the same KEM keypair. This is already a somewhat unusual situation for a real-world attack: for key agreement KEM keypairs are ephemeral; generated and used only once. Still, there are certainly legitimate use cases for long-term KEM keypairs, such as for authentication, HPKE, and in particular ECH.
The training is a key step: different devices even from the same manufacturer can have wildly different power traces running the same code. Even if two devices are of the same model, their power traces might still differ significantly.
The main contribution highlighted by the authors is that they train their neural networks to attack an implementation with 6 shares, by starting with a neural network trained to attack an implementation with 5 shares. That one can be trained from a model to attack 4 shares, and so on. Thus to apply their method, of these 150,000 power traces, one-fifth must be from an implementation with 6 shares, another one-fifth from one with 5 shares, et cetera. It seems unlikely that anyone will deploy a device where an attacker can switch between the number of shares used in the masking on demand.
Given these affordances, the attack proper can commence. The authors report that, from a single power trace of a two-share decapsulation, they could recover the shared key under these ideal circumstances with probability… 0.12%. They do not report the numbers for single trace attacks on more than two shares.
When we’re allowed multiple traces of the same decapsulation, side-channel attacks become much more effective. The second trick is a clever twist on this: instead of creating a trace of decapsulation of exactly the same message, the authors rotate the ciphertext to move bits of the shared key in more favorable positions. With 4 traces that are rotations of the same message, the success probability against the two-shares implementation goes up to 78%. The six-share implementation stands firm at 0.5%. When allowing 20 traces from the six-share implementation, the shared key can be recovered with an 87% chance.
In practice
The hardware used in the demonstration might be somewhat comparable to a smart card, but it is very different from high-end devices such as smartphones, desktop computers and servers. Simple power analysis side-channel attacks on even just embedded 1GHz processors are much more challenging, requiring tens of thousands of traces using a high-end oscilloscope connected close to the processor. There are much better avenues for attack with this kind of physical access to a server: just connect the oscilloscope to the memory bus.
Except for especially vulnerable applications, such as smart cards and HSMs, power-side channel attacks are widely considered infeasible. Although sometimes, when the planets align, an especially potent power side-channel attack can be turned into a remote timing attack due to throttling, as demonstrated by Hertzbleed. To be clear: the present attack does not even come close.
And even for these vulnerable applications, such as smart cards, this attack is not particularly potent or surprising. In the field, it is not a question of whether a masked implementation leaks its secrets, because it always does. It’s a question of how hard it is to actually pull off. Papers such as the DNG paper contribute by helping manufacturers estimate how many countermeasures to put in place, to make attacks too costly. It is not the first paper studying power side-channel attacks on Kyber and it will not be the last.
Wrapping up
AI did not completely undermine a new wave of cryptography, but instead is a helpful tool to deal with noisy data and discover the vulnerabilities within it. There is a big difference between a direct break of cryptography and a power side-channel attack. Kyber is not broken, and the presented power side-channel attack is not cause for alarm.