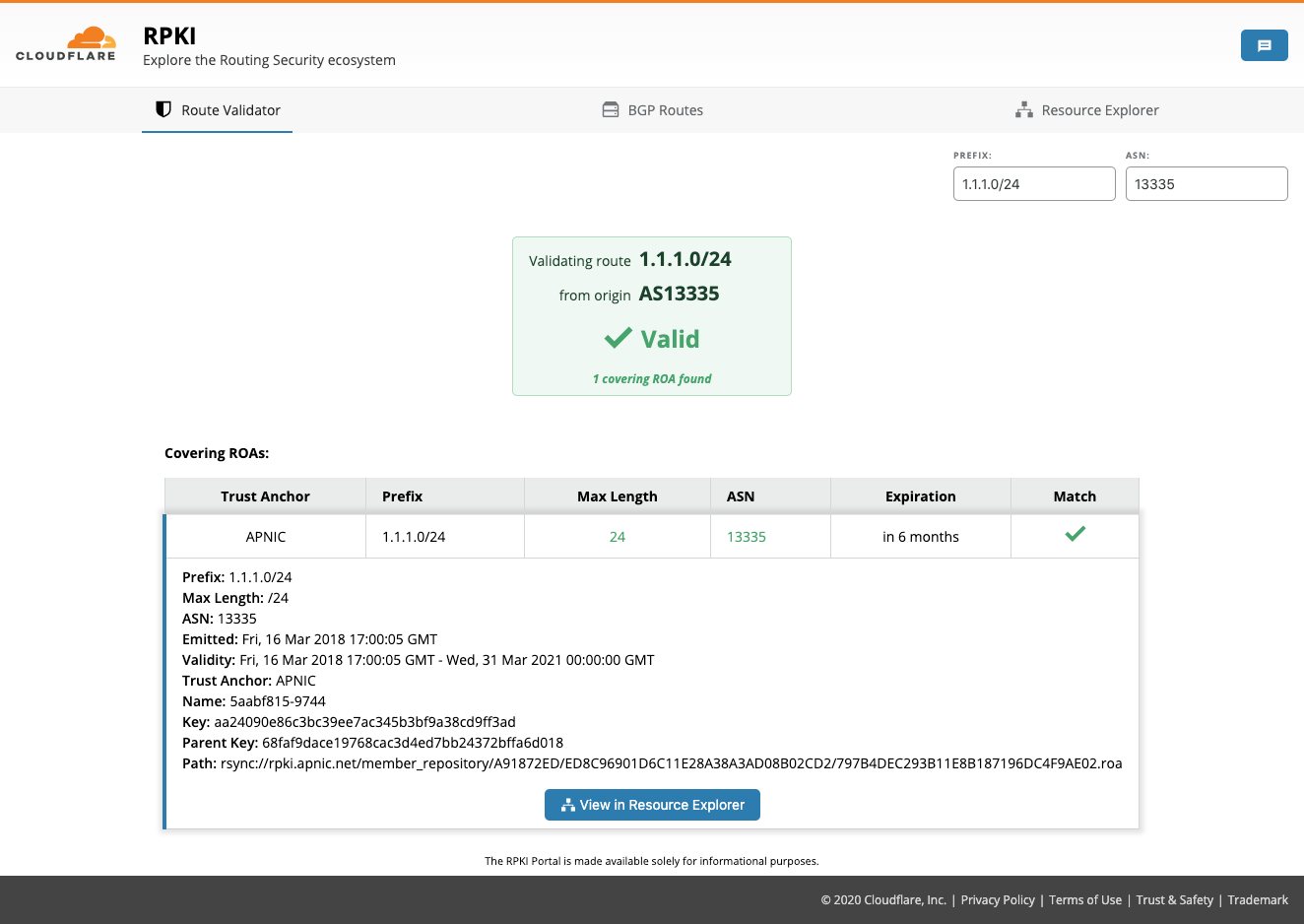
Post Syndicated from Bas Westerbaan original https://blog.cloudflare.com/sizing-up-post-quantum-signatures/
Quantum computers are a boon and a bane. Originally conceived by Manin and Feyman to simulate nature efficiently, large-scale quantum computers will speed-up innovation in material sciences by orders of magnitude. Consider the technical advances enabled by the discovery of new materials (with bronze, iron, steel and silicon each ascribed their own age!); quantum computers could help to unlock the next age of innovation. Unfortunately, they will also break the majority of the cryptography that’s currently used in TLS to protect our web browsing. They fall in two categories:
- Digital signatures, such as RSA, which ensure you’re talking to the right server.
- Key exchanges, such as Diffie–Hellman, which are used to agree on encryption keys.
A moderately-sized stable quantum computer will easily break the signatures and key exchanges currently used in TLS using Shor’s algorithm. Luckily this can be fixed: over the last two decades, there has been great progress in so-called post-quantum cryptography. “Post quantum”, abbreviated PQ, means secure against quantum computers. Five years ago, the standards institute NIST started a public process to standardise post-quantum signature schemes and key exchanges. The outcome is expected to be announced early 2022.
At Cloudflare, we’re not just following this process closely, but are also testing the real-world performance of PQ cryptography. In our 2019 experiment with Google, we saw that we can switch to a PQ key exchange with little performance impact. Among the NIST finalists, there are many with even better performance. This is good news, as we would like to switch to PQ key exchanges as soon as possible — indeed, an attacker could intercept sensitive data today, then keep and decrypt it years into the future using a quantum computer.
Why worry about PQ signatures today
One would think we can take it easy with signatures for TLS: we only need to have them replaced before a large quantum computer is built. The situation, however, is more complicated.
- The lead time to change signatures is higher. Not only do we need to change the browsers and servers, we also need to change certificate authorities (CAs) and everyone’s certificate management.
- TLS is addicted to small and fast signatures. For this page that you’re viewing we sent six signatures: two in the certificate chain; one handshake signature; one OCSP staple and finally two SCTs used for certificate transparency.
- PQ signature schemes have wildly varying performance trade-offs and quirks (as we’ll see below) which stack up quickly with six signatures, which all have slightly different requirements.
One might ask: can’t we be clever and get rid of some of these signatures? We think so! For instance, we can replace the handshake signature with a smaller key exchange or suppress intermediate certificates. Such fundamental changes take years to be adopted. That is why we are also investigating the performance of plain TLS with drop-in PQ signatures.
So, what are our options?
The zoo of PQ signatures
The three finalists of the NIST competition are Dilithium, Falcon and Rainbow. In the table below we compare them against RSA and ECDSA, both of which are in common use today, and a selection of other PQ schemes that might see standardisation in the future.
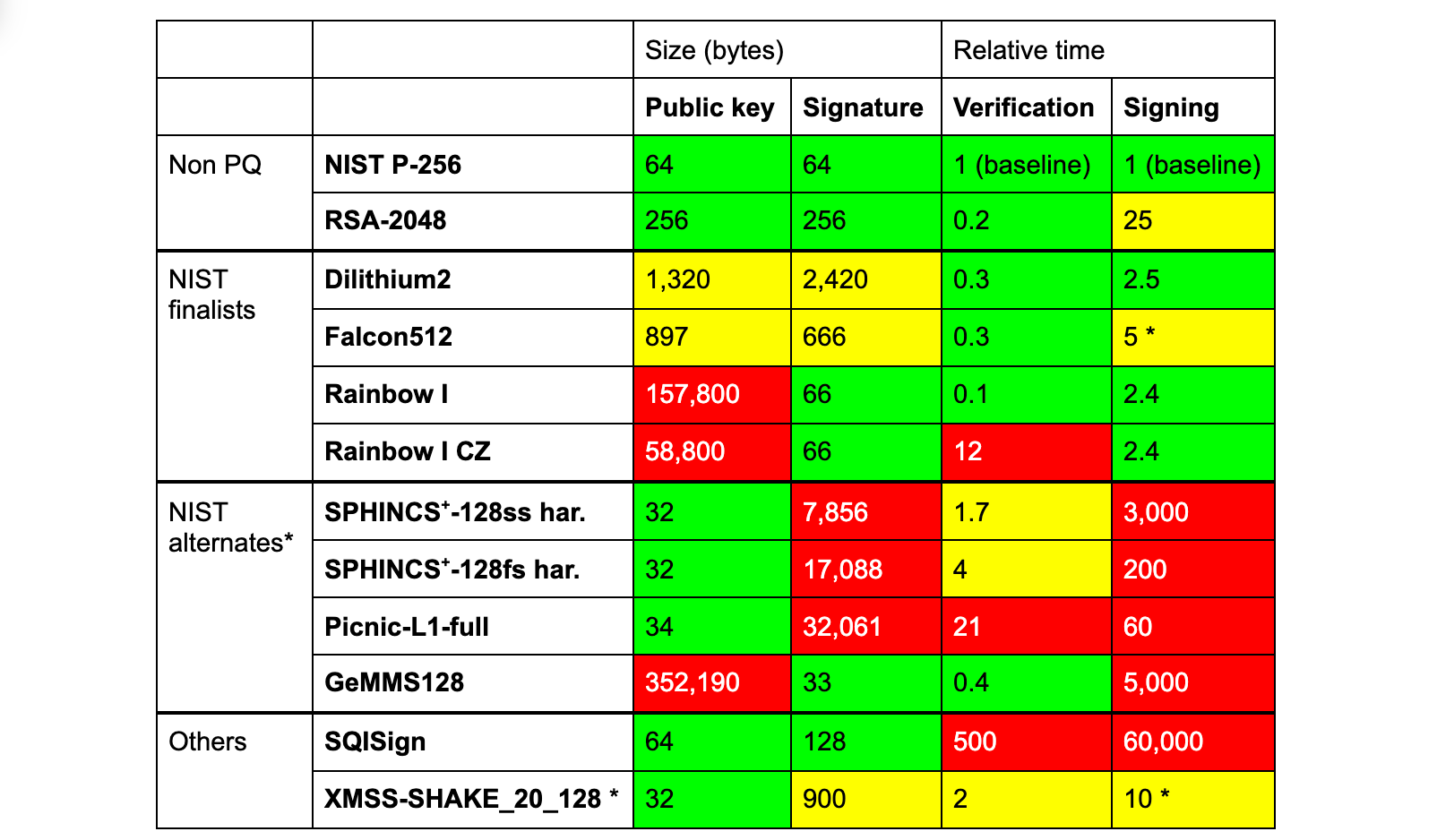
None of these PQ signatures are a clear-cut drop-in replacement. To start, all have (much) larger signatures, except for Rainbow, GeMMS and SQISign. Rainbow and GeMMS have huge public keys and SQISign is very slow.
TLS signatures
To confuse matters even more, the signatures within TLS are not all the same:
- Online. Only the handshake signature is created with every incoming TLS connection, and so signing needs to be fast. Dilithium fits this role well.
- Offline. All other signatures are made months/years in advance, and so signing time is not that important. This group splits in two:
- With a public key. The certificate chain includes signatures and their public keys. Here Falcon seems most suited.
- Without a public key. The remaining three (SCTs and OCSP staple) are just signatures. For these, Rainbow seems optimal, as its large public keys are not transmitted.
Using Dilithium, Falcon, and Rainbow, together, allows optimization for both speed and size simultaneously, which seems like a great idea. However, combining different signatures at the same time has disadvantages:
- A security issue in the design or implementation of one of the signatures compromises the whole.
- Clients need to implement multiple cryptographic algorithms, in this case three of them, which is troublesome for smaller devices — especially if separate hardware support is needed for each of them.
So do we really need to eke out every byte and every cycle of performance? Or can we stick to a single signature scheme for simplicity and security?
Can we pick just one?
If we stick to one signature scheme, looking just at the numbers, Falcon512 seems like a reasonable option. It needs 5KB of extra space (compared to a classical handshake), about the same as the Dilithium–Falcon–Rainbow chimera of before. Unfortunately Falcon comes with a caveat: creating signatures efficiently requires constant-time 64-bit floating point arithmetic. Without it, signing is 20x slower. But speed alone is not enough; it has to run in constant time. Without that, one can slowly learn the secret key by measuring the time it takes to create a signature.
Although PCs typically have a sufficiently constant-time floating-point unit, many smaller devices do not. Thus, Falcon seems ill-suited for general purpose online signatures.
What about Dilithium2? It needs 17KB extra — let’s find out if that makes a big difference.
Evidence by Experiment
All the different variables and constraints clearly complicate an already challenging puzzle. The best thing is to just try the options. Over the last few years several interesting papers have appeared studying the various options, such as SKD20, PST20, SKD21 and PKNLN22. These are great starts, but don’t provide a complete picture:
- SCTs and OCSP staples have yet to be considered. Leaving half (three) of the signatures out changes the results significantly.
- The networks tested or emulated offer insights, but are far from representative of real-world conditions. All tests were conducted between two datacenters (which does not include real-world last-mile conditions such as Wi-Fi or spotty mobile connections); or a network was simulated with unrealistic packet loss rates.
Here, Cloudflare can contribute. One of the things we like to do is to put new ideas in the community to the test on a global scale.
In this case we’re just taking a first step. Setting up a real-world experiment with a modified browser is quite involved, especially when we consider the many possible variations. Instead, as a first step, we decided first to investigate the most striking variable, the size, and try to answer the question:
How do larger signatures affect the TLS handshake?
There are two parts to this: how fast are they, and, more importantly, do they work at all?
Experimental setup
We need some way to emulate bigger signatures without having to modify the clients. We considered several options. The first idea we had was to pad a valid certificate with a dummy extension. That would require a custom certificate for each size to test, which is cumbersome. Then we considered responding with a dummy ServerHello extension. This is, however, not allowed by TLS 1.2 without a corresponding ClientHello extension. In the end, we went for adding dummy certificates.
Dummy certificates
These dummy certificates are 1kB self-signed invalid certificates that have nothing to do with the certificate chain. To vary the size to test, we simply add more copies. Adding unrelated certificates to the certificate chain is a common misconfiguration and clients have learnt to ignore them. In fact, TLS 1.3 stipulates that these (in rfc-speak) SHOULD be ignored by the client. Testing out hundreds of browsers, we saw no issues.
Standards and reality don’t always agree: when inserting dummy certificates on actual traffic, we saw issues with a small, but not insignificant number of clients. We don’t want to ruin anyone’s connection, and so we decided to use separate connections for this purpose.
Using challenge pages to launch probes
So what did we actually do? On a small percentage of the challenge pages (those with the CAPTCHA), we pick a number n and a random key and send this key in two separate background requests to:
0.tls-size-experiment-c.cloudflareresearch.com[n].tls-size-experiment-1.cloudflareresearch.com
The first, the control, is a normal webpage that stores the TLS handshake time under the key that’s been sent. The real action happens at the second, the live, which adds the n dummy certificates to its chain. The live also stores handshake time under the given key. We could call it “experimental” instead of “live”, but the benign control connection is also an important part of the experiment. Indeed, it allows us to see if live connections are missing. These endpoints were a breeze to write using Cloudflare Workers and KV.
How much dummy data to test?
Before launching the experiment, we tested several libraries and browsers on the live endpoint to see whether they would error due to the dummy certificates. None rejected a single certificate, but how far can we go? TLS 1.3 theoretically allows a certificate chain of 16MB, but in practice many clients reject a much shorter chain. OpenSSL, for instance, rejects one of 102kB. The most stingy we found is Go’s TLS client, which rejects a handshake larger than 64kB. Because of this, we tested with between 1 and 59 dummy certificates.
Intermezzo: TCP’s congestion window
So, what did we find? The graphs are in the next section, have a peek! Before diving right in, we would like to explain a crucial concept, the TCP congestion window, that helps us read the results.
Data sent over the Internet is broken down in packets of around 1.4kB that traverse many routers to reach their destination. Sometimes a router has more incoming packets than it can handle and it has to drop them — this is called congestion. To avoid causing congestion, TCP initially sends just a few packets (typically ten, so ~14kB). Then, with every acknowledgement received in return, the TCP sender will very quickly ramp up the number of packets that it keeps in flight. This number is called the congestion window (cwnd). When it gets too high, congestion occurs, packets are dropped and in response the sender backs off by dialing down the congestion window. Any dropped packet is seen as a sign of congestion by TCP. For this reason, Wi-Fi has its own retransmission mechanism transparent to TCP.
Considering all this, we would expect to see two effects with larger signatures:
- Gentle slope. Every single packet needs some extra time to transmit, due to limited bandwidth and possible physical-layer retransmissions. This slope isn’t so gentle if your internet connection is slow or spotty.
- cwnd wall. Once we fill the congestion window, we have to wait for a whole roundtrip before we can continue. This effect is stronger if the roundtrip time (RTT) is higher.
The strength of the two effects can differ. With a fast connection and high RTT we expect to see the graph below on the left. With a slow connection and low RTT, we expect the one on the right.
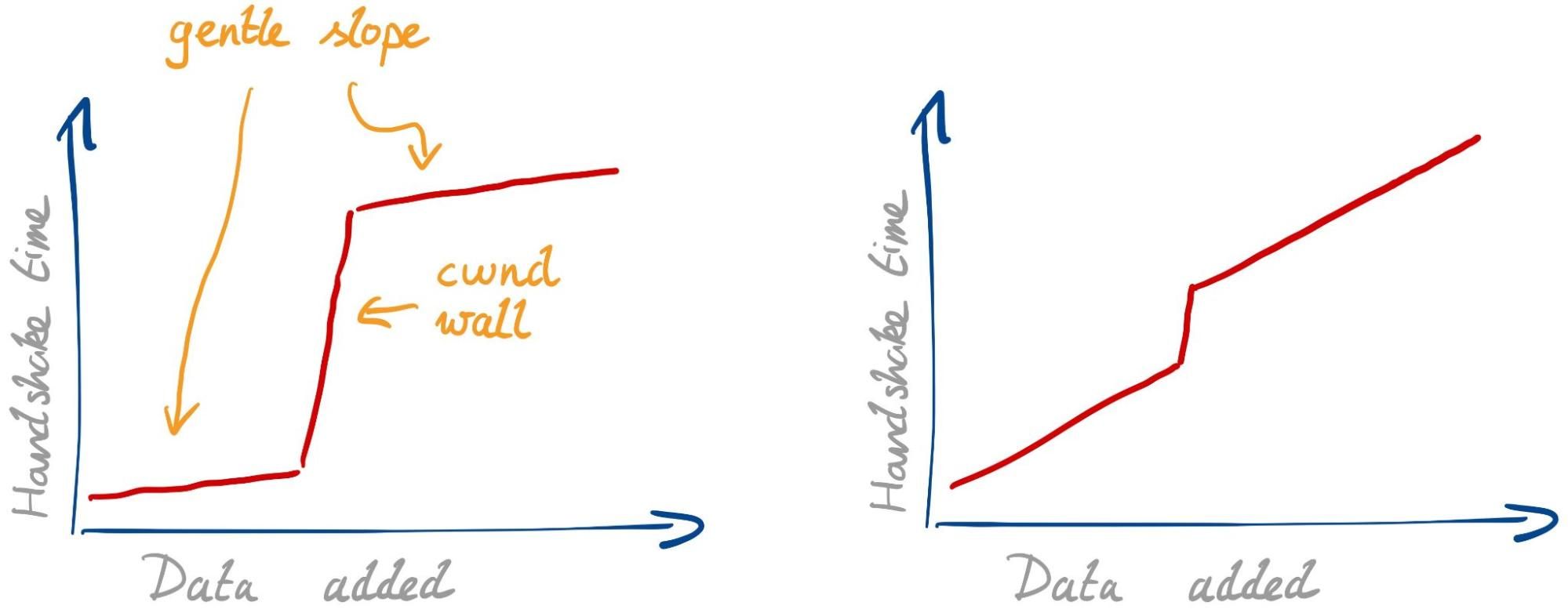
There might be other unknown effects. The best thing is to have a look.
In PQ research, the second effect has gained the most attention. The larger signatures simply do not fit in the initial congestion windows used today. A common suggestion in response has been to simply increase the initial congestion window to accommodate the larger signatures. This is far from a simple change to make globally, and we have to understand if this solves the problem to begin with.
Results
Over 24 days we’ve received 964,499 live connections from 454,218 different truncated IPs (to 24 bits, “/24”, for IPv4 and 48 bits for IPv6) and 11,239 different ASNs. First, let’s check how many clients had trouble with the bigger handshakes.
Can clients handle the larger handshakes?
The control connection was missing for 2.4% of the live connections. This is not alarming: we expect some connections to be missing for harmless reasons, such as the user browsing away from the challenge page. There are, however, significantly more live connections without control connection at 3.6%.
In the graph below on the left we break the number of received live connections down by the number of dummy certificates added. Because we pick the number of certificates randomly, the graph is noisy. To get a clearer picture, we started storing the number of certificates added in the corresponding control request, which gives us the graph on the right. The bumps at 10kB and 30kB suggest that there are clients or middleboxes that cannot handle these handshake sizes.
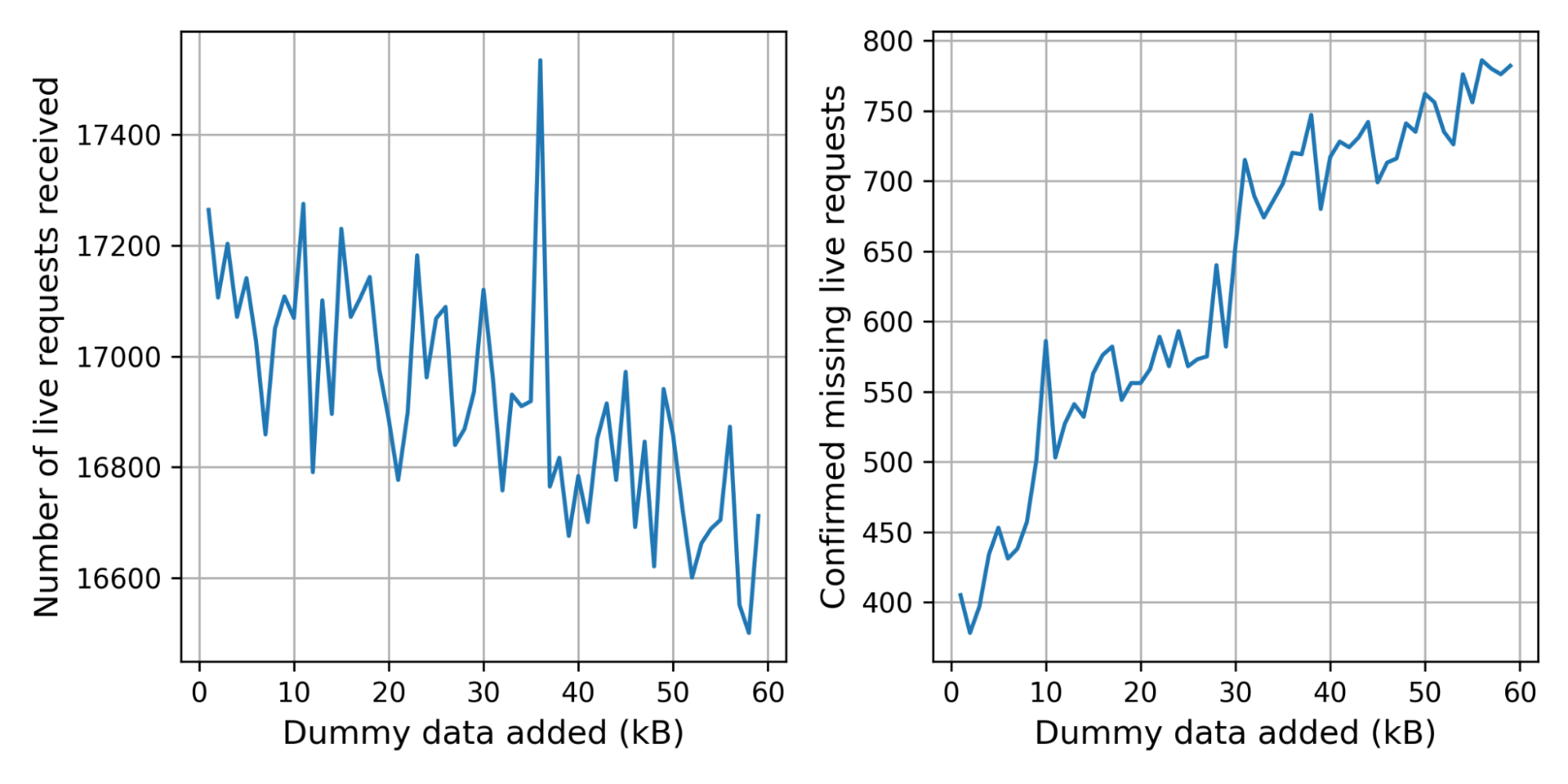
Handshake times with larger signatures
What is the effect on the handshake time? The graph on the left shows the weighted median and 75th percentile TLS handshake times for different amounts of dummy data added. We use the weight so that every truncated IP contributes equally. On the right we show the slowdowns for each size, relative to the handshake time of the control connection.
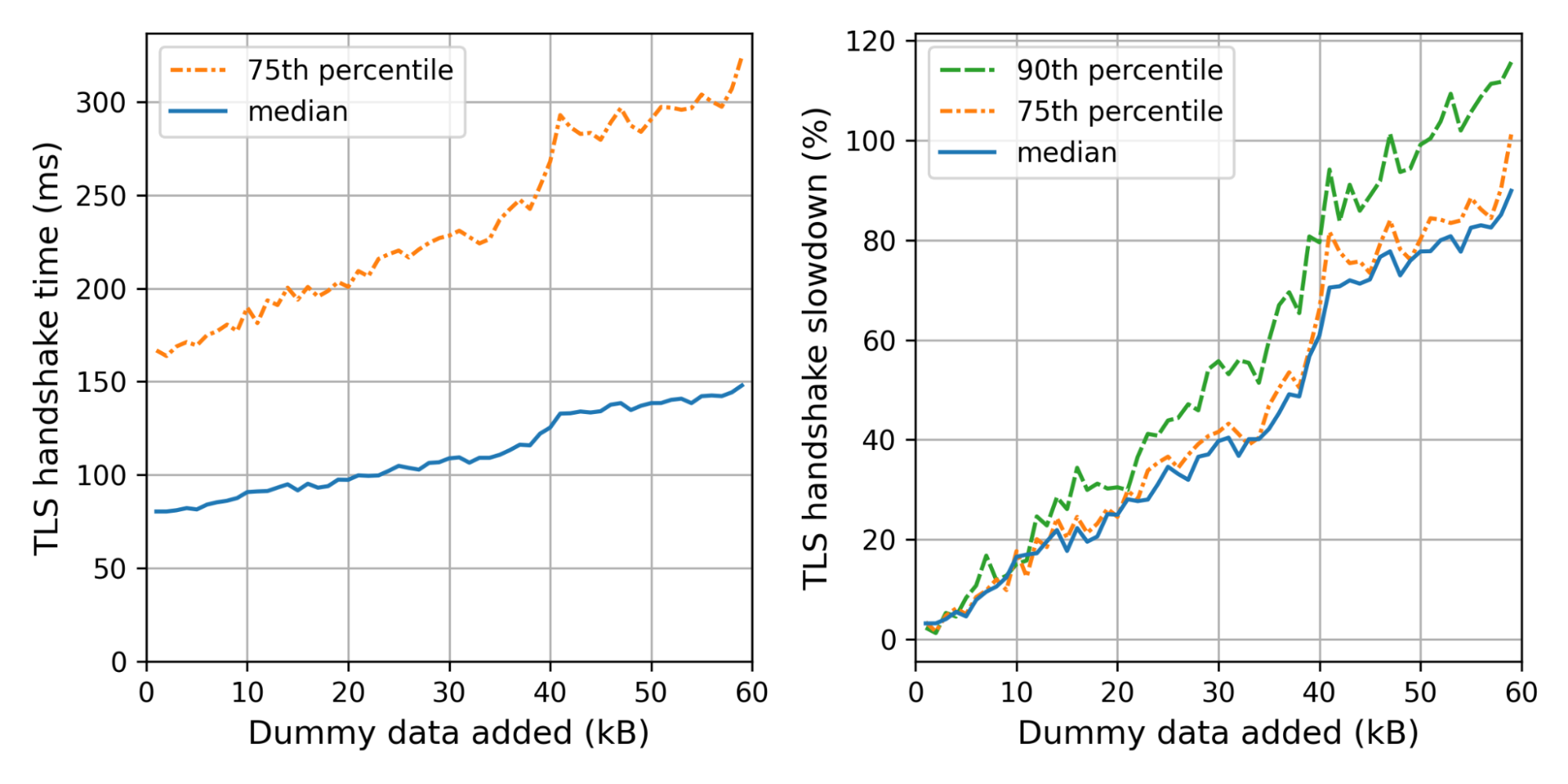
We can see the not-so-gentle slope until 40kB, where we hit a little wall that corresponds to Cloudflare’s default initial congestion window of 30 packets.
Adding 35kB fits within our initial congestion window. Nonetheless, the median handshake with 35kB extra is 40% slower. The slowest 10% are even worse off, taking 60% as much time. Thus even though we stay within the congestion window, the added data is not for free at all.
We can now translate these insights back to concrete PQ signatures. For example, using Dilithium2 as a drop-in replacement, we need around 17kB extra. That also fits within our initial congestion window with a median slowdown of 20%, which gets worse for the tail-end of users. For the normal initial congestion window of ten, we expect the slowdown to be much worse — around 60–80%.
There are several caveats to point out:
- These experiments used an initial congestion window of 30 packets instead of ten. With a smaller initial congestion window of ten, which is the default for most systems, we would expect the wall to move from 40kB to around 10kB.
- Because of our presence all across the world, our RTTs are fairly low. Thus the effect of the cwnd wall is smaller for us.
- Challenge pages are served, by design, to those clients that we expect to be bots. This adds a significant bias because bots are generally hosted at well-connected providers, and so are closer than users.
- HTTP/3 was not supported by the server we used for the endpoint. Support for IPv6 was only added ten days into the experiment and accounts for 10.9% of the measurements.
- Actual TLS handshakes differ in size much more than tested in this setup due to differences in certificate sizes and extensions and other factors.
What have we learned?
The TLS handshake is just one step (~5–20%) in a long chain required to show you a webpage. Casually browsing, it would be hard to notice a TLS handshake that’s 60% slower. But such differences add up. To make a website really fast, you need many seemingly insignificant speedups. Browser developers take this seriously: only in exceptional cases does Chrome allow a change that slows down any microbenchmark by even a percent.
Because of the many parties and complexities involved, we should avoid waiting too long to adopt post-quantum signatures in TLS. That’s a hard sell if it comes at the price of a double-digit slowdown, not least to content servers but also to browser vendors and clients.
A timely adoption of PQ signatures on the web would be great. Our evidence so far suggests that this will be easiest, if six signatures and two public keys would fit in 9kB.
We will continue our efforts to help build a post-quantum secure Internet. To follow along, keep an eye on this blog or have a look at research.cloudflare.com.
Bas Westerbaan is co-submitter of the SPHINCS+ signature scheme.
References
SKD20: Sikeridis, Kampanakis, Devetsikiotis. Assessing the overhead of post-quantum cryptography in TLS 1.3 and SSH. CoNEXT’20.
PST20: Paquin, Stebila, Tamvada. Benchmarking Post-Quantum Cryptography in TLS. PQCrypto 2020.
SKD21: Sikeridis, Kampanakis, Devetsikiotis. Post-Quantum Authentication in TLS 1.3: A Performance Study. NDSS2020.
PKNLN22: Paul, Kuzovkova, Lahr, Niederhagen. Mixed Certificate Chains for the Transition to Post-Quantum Authentication in TLS 1.3. To appear in AsiaCCS 2022.