Tag Archives: TLS

Encryption in transit over external networks: AWS guidance for NYDFS and beyond

Post Syndicated from Aravind Gopaluni original https://aws.amazon.com/blogs/security/encryption-in-transit-over-external-networks-aws-guidance-for-nydfs-and-beyond/

On November 1, 2023, the New York State Department of Financial Services (NYDFS) issued its Second Amendment (the Amendment) to its Cybersecurity Requirements for Financial Services Companies adopted in 2017, published within Section 500 of 23 NYCRR 500 (the Cybersecurity Requirements; the Cybersecurity Requirements as amended by the Amendment, the Amended Cybersecurity Requirements). In the introduction to its Cybersecurity Resource Center, the Department explains that the revisions are aimed at addressing the changes in the increasing sophistication of threat actors, the prevalence of and relative ease in running cyberattacks, and the availability of additional controls to manage cyber risks.

This blog post focuses on the revision to the encryption in transit requirement under section 500.15(a). It outlines the encryption capabilities and secure connectivity options offered by Amazon Web Services (AWS) to help customers demonstrate compliance with this updated requirement. The post also provides best practices guidance, emphasizing the shared responsibility model. This enables organizations to design robust data protection strategies that address not only the updated NYDFS encryption requirements but potentially also other security standards and regulatory requirements.

The target audience for this information includes security leaders, architects, engineers, and security operations team members and risk, compliance, and audit professionals.

Note that the information provided here is for informational purposes only; it is not legal or compliance advice and should not be relied on as legal or compliance advice. Customers are responsible for making their own independent assessments and should obtain appropriate advice from their own legal and compliance advisors regarding compliance with applicable NYDFS regulations.

500.15 Encryption of nonpublic information

The updated requirement in the Amendment states that:

  1. As part of its cybersecurity program, each covered entity shall implement a written policy requiring encryption that meets industry standards, to protect nonpublic information held or transmitted by the covered entity both in transit over external networks and at rest.
  2. To the extent a covered entity determines that encryption of nonpublic information at rest is infeasible, the covered entity may instead secure such nonpublic information using effective alternative compensating controls that have been reviewed and approved by the covered entity’s CISO in writing. The feasibility of encryption and effectiveness of the compensating controls shall be reviewed by the CISO at least annually.

This section of the Amendment removes the covered entity’s chief information security officer’s (CISO) discretion to approve compensating controls when encryption of nonpublic information in transit over external networks is deemed infeasible. The Amendment mandates that, effective November 2024, organizations must encrypt nonpublic information transmitted over external networks without the option of implementing alternative compensating controls. While the use of security best practices such as network segmentation, multi-factor authentication (MFA), and intrusion detection and prevention systems (IDS/IPS) can provide defense in depth, these compensating controls are no longer sufficient to replace encryption in transit over external networks for nonpublic information.

However, the Amendment still allows for the CISO to approve the use of alternative compensating controls where encryption of nonpublic information at rest is deemed infeasible. AWS is committed to providing industry-standard encryption services and capabilities to help protect customer data at rest in the cloud, offering customers the ability to add layers of security to their data at rest, providing scalable and efficient encryption features. This includes the following services:

While the above highlights encryption-at-rest capabilities offered by AWS, the focus of this blog post is to provide guidance and best practice recommendations for encryption in transit.

AWS guidance and best practice recommendations

Cloud network traffic encompasses connections to and from the cloud and traffic between cloud service provider (CSP) services. From an organization’s perspective, CSP networks and data centers are deemed external because they aren’t under the organization’s direct control. The connection between the organization and a CSP, typically established over the internet or dedicated links, is considered an external network. Encrypting data in transit over these external networks is crucial and should be an integral part of an organization’s cybersecurity program.

AWS implements multiple mechanisms to help ensure the confidentiality and integrity of customer data during transit and at rest across various points within its environment. While AWS employs transparent encryption at various transit points, we strongly recommend incorporating encryption by design into your architecture. AWS provides robust encryption-in-transit capabilities to help you adhere to compliance requirements and mitigate the risks of unauthorized disclosure and modification of nonpublic information in transit over external networks.

Additionally, AWS recommends that financial services institutions adopt a secure by design (SbD) approach to implement architectures that are pre-tested from a security perspective. SbD helps establish control objectives, security baselines, security configurations, and audit capabilities for workloads running on AWS.

Security and Compliance is a shared responsibility between AWS and the customer. Shared responsibility can vary depending on the security configuration options for each service. You should carefully consider the services you choose because your organization’s responsibilities vary depending on the services used, the integration of those services into your IT environment, and applicable laws and regulations. AWS provides resources such as service user guides and AWS Customer Compliance Guides, which map security best practices for individual services to leading compliance frameworks, including NYDFS.

Protecting connections to and from AWS

We understand that customers place a high priority on privacy and data security. That’s why AWS gives you ownership and control over your data through services that allow you to determine where your content will be stored, secure your content in transit and at rest, and manage access to AWS services and resources for your users. When architecting workloads on AWS, classifying data based on its sensitivity, criticality, and compliance requirements is essential. Proper data classification allows you to implement appropriate security controls and data protection mechanisms, such as Transport Layer Security (TLS) at the application layer, access control measures, and secure network connectivity options for nonpublic information over external networks. When it comes to transmitting nonpublic information over external networks, it’s a recommended practice to identify network segments traversed by this data based on your network architecture. While AWS employs transparent encryption at various transit points, it’s advisable to implement encryption solutions at multiple layers of the OSI model to establish defense in depth and enhance end-to-end encryption capabilities. Although requirement 500.15 of the Amendment doesn’t mandate end-to-end encryption, implementing such controls can provide an added layer of security and can help demonstrate that nonpublic information is consistently encrypted during transit.

AWS offers several options to achieve this. While not every option provides end-to-end encryption on its own, using them in combination helps to ensure that nonpublic information doesn’t traverse open, public networks unprotected. These options include:

  • Using AWS Direct Connect with IEEE 802.1AE MAC Security Standard (MACsec) encryption
  • VPN connections
  • Secure API endpoints
  • Client-side encryption of data before sending it to AWS

AWS Direct Connect with MACsec encryption

AWS Direct Connect provides direct connectivity to the AWS network through third-party colocation facilities, using a cross-connect between an AWS owned device and either a customer- or partner-owned device. Direct Connect can reduce network costs, increase bandwidth throughput, and provide a more consistent network experience than internet-based connections. Within Direct Connect connections (a physical construct) there will be one or more virtual interfaces (VIFs). These are logical entities and are reflected as industry-standard 802.1Q VLANs on the customer equipment terminating the Direct Connect connection. Depending on the type of VIF, they will use either public or private IP addressing. There are three different types of VIFs:

  • Public virtual interface – Establish connectivity between AWS public endpoints and your data center, office, or colocation environment.
  • Transit virtual interface – Establish private connectivity between AWS Transit Gateways and your data center, office, or colocation environment. Transit Gateways is an AWS managed high availability and scalability regional network transit hub used to interconnect Amazon Virtual Private Cloud (Amazon VPC) and customer networks.
  • Private virtual interface – Establish private connectivity between Amazon VPC resources and your data center, office, or colocation environment.

By default, a Direct Connect connection isn’t encrypted from your premises to the Direct Connect location because AWS cannot assume your on-premises device supports the MACsec protocol. With MACsec, Direct Connect delivers native, near line-rate, point-to-point encryption, ensuring that data communications between AWS and your corporate network remain protected. MACsec is supported on 10 Gbps and 100 Gbps dedicated Direct Connect connections at selected points of presence. Using Direct Connect with MACsec-enabled connections and combining it with the transparent physical network encryption offered by AWS from the Direct Connect location through the AWS backbone not only benefits you by allowing you to securely exchange data with AWS, but also enables you to use the highest available bandwidth. For additional information on MACsec support and cipher suites, see the MACsec section in the Direct Connect FAQs.

Figure 1 illustrates a sample reference architecture for securing traffic from corporate network to your VPCs over Direct Connect with MACsec and AWS Transit Gateways.

Figure 1: Sample architecture for using Direct Connect with MACsec encryption

Figure 1: Sample architecture for using Direct Connect with MACsec encryption

In the sample architecture, you can see that Layer 2 encryption through MACsec only encrypts the traffic from your on-premises systems to the AWS device in the Direct Connect location, and therefore you need to consider additional encryption solutions at Layer 3, 4, or 7 to get closer to end-to-end encryption to the device where you’re comfortable for the packets to be decrypted. In the next section, let’s review an option for using network layer encryption using AWS Site-to-Site VPN.

Direct Connect with Site-to-Site VPN

AWS Site-to-Site VPN is a fully managed service that creates a secure connection between your corporate network and your Amazon VPC using IP security (IPsec) tunnels over the internet. Data transferred between your VPC and the remote network routes over an encrypted VPN connection to help maintain the confidentiality and integrity of data in transit. Each VPN connection consists of two tunnels between a virtual private gateway or transit gateway on the AWS side and a customer gateway on the on-premises side. Each tunnel supports a maximum throughput of up to 1.25 Gbps. See Site-to-Site VPN quotas for more information.

You can use Site-to-Site VPN over Direct Connect to achieve secure IPsec connection with the low latency and consistent network experience of Direct Connect when reaching resources in your Amazon VPCs.

Figure 2 illustrates a sample reference architecture for establishing end-to-end IPsec-encrypted connections between your networks and Transit Gateway over a private dedicated connection.

Figure 2: Encrypted connections between the AWS Cloud and a customer’s network using VPN

Figure 2: Encrypted connections between the AWS Cloud and a customer’s network using VPN

While Direct Connect with MACsec and Site-to-Site VPN with IPsec can provide encryption at the physical and network layers respectively, they primarily secure the data in transit between your on-premises network and the AWS network boundary. To further enhance the coverage for end-to-end encryption, it is advisable to use TLS encryption. In the next section, let’s review mechanisms for securing API endpoints on AWS using TLS encryption.

Secure API endpoints

APIs act as the front door for applications to access data, business logic, or functionality from other applications and backend services.

AWS enables you to establish secure, encrypted connections to its services using public AWS service API endpoints. Public AWS owned service API endpoints (AWS managed services like Amazon Simple Queue Service (Amazon SQS), AWS Identity and Access Management (IAM), AWS Key Management Service (AWS KMS), others) have certificates that are owned and deployed by AWS. By default, requests to these public endpoints use HTTPS. To align with evolving technology and regulatory standards for TLS, as of February 27, 2024, AWS has updated its TLS policy to require a minimum of TLS 1.2, thereby deprecating support for TLS 1.0 and 1.1 versions on AWS service API endpoints across each of our AWS Regions and Availability Zones.

Additionally, to enhance connection performance, AWS has begun enabling TLS version 1.3 globally for its service API endpoints. If you’re using the AWS SDKs or AWS Command Line Interface (AWS CLI), you will automatically benefit from TLS 1.3 after a service enables it.

While requests to public AWS service API endpoints use HTTPS by default, a few services, such as Amazon S3 and Amazon DynamoDB, allow using either HTTP or HTTPS. If the client or application chooses HTTP, the communication isn’t encrypted. Customers are responsible for enforcing HTTPS connections when using such AWS services. To help ensure secure communication, you can establish an identity perimeter by using the IAM policy condition key aws:SecureTransport in your IAM roles to evaluate the connection and mandate HTTPS usage.

As enterprises increasingly adopt cloud computing and microservices architectures, teams frequently build and manage internal applications exposed as private API endpoints. Customers are responsible for managing the certificates on private customer-owned endpoints. AWS helps you deploy private customer-owned identities (that is, TLS certificates) through the use of AWS Certificate Manager (ACM) private certificate authorities (PCA) and the integration with AWS services that offer private customer-owned TLS termination endpoints.

ACM is a fully managed service that lets you provision, manage, and deploy public and private TLS certificates for use with AWS services and internal connected resources. ACM minimizes the time-consuming manual process of purchasing, uploading, and renewing TLS certificates. You can provide certificates for your integrated AWS services either by issuing them directly using ACM or by importing third-party certificates into the ACM management system. ACM offers two options for deploying managed X.509 certificates. You can choose the best one for your needs.

  • AWS Certificate Manager (ACM) – This service is for enterprise customers who need a secure web presence using TLS. ACM certificates are deployed through Elastic Load Balancing (ELB), Amazon CloudFront, Amazon API Gateway, and other integrated AWS services. The most common application of this type is a secure public website with significant traffic requirements. ACM also helps to simplify security management by automating the renewal of expiring certificates.
  • AWS Private Certificate Authority (Private CA) – This service is for enterprise customers building a public key infrastructure (PKI) inside the AWS Cloud and is intended for private use within an organization. With AWS Private CA, you can create your own certificate authority (CA) hierarchy and issue certificates with it for authenticating users, computers, applications, services, servers, and other devices. Certificates issued by a private CA cannot be used on the internet. For more information, see the AWS Private CA User Guide.

You can use a centralized API gateway service, such as Amazon API Gateway, to securely expose customer-owned private API endpoints. API Gateway is a fully managed service that allows developers to create, publish, maintain, monitor, and secure APIs at scale. With API Gateway, you can create RESTful APIs and WebSocket APIs, enabling near real-time, two-way communication applications. API Gateway operations must be encrypted in-transit using TLS, and require the use of HTTPS endpoints. You can use API Gateway to configure custom domains for your APIs using TLS certificates provisioned and managed by ACM. Developers can optionally choose a specific TLS version for their custom domain names. For use cases that require mutual TLS (mTLS) authentication, you can configure certificate-based mTLS authentication on your custom domains.

Pre-encryption of data to be sent to AWS

Depending on the risk profile and sensitivity of the data that’s being transferred to AWS, you might want to choose encrypting data in an application running on your corporate network before sending it to AWS (client-side encryption). AWS offers a variety of SDKs and client-side encryption libraries to help you encrypt and decrypt data in your applications. You can use these libraries with the cryptographic service provider of your choice, including AWS Key Management Service or AWS CloudHSM, but the libraries do not require an AWS service.

  • The AWS Encryption SDK is a client-side encryption library that you can use to encrypt and decrypt data in your application and is available in several programming languages, including a command-line interface. You can use the SDK to encrypt your data before you send it to an AWS service. The SDK offers advanced data protection features, including envelope encryption and additional authenticated data (AAD). It also offers secure, authenticated, symmetric key algorithm suites, such as 256-bit AES-GCM with key derivation and signing.
  • The AWS Database Encryption SDK is a set of software libraries developed in open source that enable you to include client-side encryption in your database design. The SDK provides record-level encryption solutions. You specify which fields are encrypted and which fields are included in the signatures that help ensure the authenticity of your data. Encrypting your sensitive data in transit and at rest helps ensure that your plaintext data isn’t available to a third party, including AWS. The AWS Database Encryption SDK for DynamoDB is designed especially for DynamoDB applications. It encrypts the attribute values in each table item using a unique encryption key. It then signs the item to protect it against unauthorized changes, such as adding or deleting attributes or swapping encrypted values. After you create and configure the required components, the SDK transparently encrypts and signs your table items when you add them to a table. It also verifies and decrypts them when you retrieve them. Searchable encryption in the AWS Database Encryption SDK enables you search encrypted records without decrypting the entire database. This is accomplished by using beacons, which create a map between the plaintext value written to a field and the encrypted value that is stored in your database. For more information, see the AWS Database Encryption SDK Developer Guide.
  • The Amazon S3 Encryption Client is a client-side encryption library that enables you to encrypt an object locally to help ensure its security before passing it to Amazon S3. It integrates seamlessly with the Amazon S3 APIs to provide a straightforward solution for client-side encryption of data before uploading to Amazon S3. After you instantiate the Amazon S3 Encryption Client, your objects are automatically encrypted and decrypted as part of your Amazon S3 PutObject and GetObject requests. Your objects are encrypted with a unique data key. You can use both the Amazon S3 Encryption Client and server-side encryption to encrypt your data. The Amazon S3 Encryption Client is supported in a variety of programming languages and supports industry-standard algorithms for encrypting objects and data keys. For more information, see the Amazon S3 Encryption Client developer guide.

Encryption in-transit inside AWS

AWS implements responsible and sophisticated technical and physical controls that are designed to help prevent unauthorized access to or disclosure of your content. To protect data in transit, traffic traversing through the AWS network that is outside of AWS physical control is transparently encrypted by AWS at the physical layer. This includes traffic between AWS Regions (except China Regions), traffic between Availability Zones, and between Direct Connect locations and Regions through the AWS backbone network.

Network segmentation

When you create an AWS account, AWS offers a virtual networking option to launch resources in a logically isolated virtual private network (VPN), Amazon Virtual Private Cloud (Amazon VPC). A VPC is limited to a single AWS Region and every VPC has one or more subnets. VPCs can be connected externally using an internet gateway (IGW), VPC peering connection, VPN, Direct Connect, or Transit Gateways. Traffic within the your VPC is considered internal because you have complete control over your virtual networking environment, including selection of your own IP address range, creation of subnets, and configuration of route tables and network gateways.

As a customer, you maintain ownership of your data, and you select which AWS services can process, store, and host your data, and you choose the Regions in which your data is stored. AWS doesn’t automatically replicate data across Regions, unless the you choose to do so. Data transmitted over the AWS global network between Regions and Availability Zones is automatically encrypted at the physical layer before leaving AWS secured facilities. Cross-Region traffic that uses Amazon VPC and Transit Gateway peering is automatically bulk-encrypted when it exits a Region.

Encryption between instances

AWS provides secure and private connectivity between Amazon Elastic Compute Cloud (Amazon EC2) instances of all types. The Nitro System is the underlying foundation for modern Amazon EC2 instances. It’s a combination of purpose-built server designs, data processors, system management components, and specialized firmware that provides the underlying foundation for EC2 instances launched since the beginning of 2018. Instance types that use the offload capabilities of the underlying Nitro System hardware automatically encrypt in-transit traffic between instances. This encryption uses Authenticated Encryption with Associated Data (AEAD) algorithms, with 256-bit encryption and has no impact on network performance. To support this additional in-transit traffic encryption between instances, instances must be of supported instance types, in the same Region, and in the same VPC or peered VPCs. For a list of supported instance types and additional requirements, see Encryption in transit.

Conclusion

The second Amendment to the NYDFS Cybersecurity Regulation underscores the criticality of safeguarding nonpublic information during transmission over external networks. By mandating encryption for data in transit and eliminating the option for compensating controls, the Amendment reinforces the need for robust, industry-standard encryption measures to protect the confidentiality and integrity of sensitive information.

AWS provides a comprehensive suite of encryption services and secure connectivity options that enable you to design and implement robust data protection strategies. The transparent encryption mechanisms that AWS has built into services across its global network infrastructure, secure API endpoints with TLS encryption, and services such as Direct Connect with MACsec encryption and Site-to-Site VPN, can help you establish secure, encrypted pathways for transmitting nonpublic information over external networks.

By embracing the principles outlined in this blog post, financial services organizations can address not only the updated NYDFS encryption requirements for section 500.15(a) but can also potentially demonstrate their commitment to data security across other security standards and regulatory requirements.

For further reading on considerations for AWS customers regarding adherence to the Second Amendment to the NYDFS Cybersecurity Regulation, see the AWS Compliance Guide to NYDFS Cybersecurity Regulation.

If you have feedback about this post, submit comments in the Comments section below. If you have questions about this post, start a new thread on the AWS Financial Services re:Post and AWS Security, Identity, & Compliance re:Post ,or contact AWS Support.
 

Aravind Gopaluni
Aravind Gopaluni

Aravind is a Senior Security Solutions Architect at AWS, helping financial services customers navigate ever-evolving cloud security and compliance needs. With over 20 years of experience, he has honed his expertise in delivering robust solutions to numerous global enterprises. Away from the world of cybersecurity, he cherishes traveling and exploring cuisines with his family.
Stephen Eschbach
Stephen Eschbach

Stephen is a Senior Compliance Specialist at AWS, helping financial services customers meet their security and compliance objectives on AWS. With over 18 years of experience in enterprise risk, IT GRC, and IT regulatory compliance, Stephen has worked and consulted for several global financial services companies. Outside of work, Stephen enjoys family time, kids’ sports, fishing, golf, and Texas BBQ.

Introducing Automatic SSL/TLS: securing and simplifying origin connectivity

Post Syndicated from Alex Krivit original https://blog.cloudflare.com/introducing-automatic-ssl-tls-securing-and-simplifying-origin-connectivity


During Birthday Week 2022, we pledged to provide our customers with the most secure connection possible from Cloudflare to their origin servers automatically. I’m thrilled to announce we will begin rolling this experience out to customers who have the SSL/TLS Recommender enabled on August 8, 2024. Following this, remaining Free and Pro customers can use this feature beginning September 16, 2024, with Business and Enterprise customers to follow.

Although it took longer than anticipated to roll out, our priority was to achieve an automatic configuration both transparently and without risking any site downtime. Taking this additional time allowed us to balance enhanced security with seamless site functionality, especially since origin server security configuration and capabilities are beyond Cloudflare’s direct control. The new Automatic SSL/TLS setting will maximize and simplify the encryption modes Cloudflare uses to communicate with origin servers by using the SSL/TLS Recommender.

We first talked about this process in 2014: at that time, securing connections was hard to configure, prohibitively expensive, and required specialized knowledge to set up correctly. To help alleviate these pains, Cloudflare introduced Universal SSL, which allowed web properties to obtain a free SSL/TLS certificate to enhance the security of connections between browsers and Cloudflare.

This worked well and was easy because Cloudflare could manage the certificates and connection security from incoming browsers. As a result of that work, the number of encrypted HTTPS connections on the entire Internet doubled at that time. However, the connections made from Cloudflare to origin servers still required manual configuration of the encryption modes to let Cloudflare know the capabilities of the origin.

Today we’re excited to begin the sequel to Universal SSL and make security between Cloudflare and origins automatic and easy for everyone.

History of securing origin-facing connections

Ensuring that more bytes flowing across the Internet are automatically encrypted strengthens the barrier against interception, throttling, and censorship of Internet traffic by third parties.

Generally, two communicating parties (often a client and server) establish a secure connection using the TLS protocol. For a simplified breakdown:

  • The client advertises the list of encryption parameters it supports (along with some metadata) to the server.
  • The server responds back with its own preference of the chosen encryption parameters. It also sends a digital certificate so that the client can authenticate its identity.
  • The client validates the server identity, confirming that the server is who it says it is.
  • Both sides agree on a symmetric secret key for the session that is used to encrypt and decrypt all transmitted content over the connection.

Because Cloudflare acts as an intermediary between the client and our customer’s origin server, two separate TLS connections are established. One between the user’s browser and our network, and the other from our network to the origin server. This allows us to manage and optimize the security and performance of both connections independently.

Unlike securing connections between clients and Cloudflare, the security capabilities of origin servers are not under our direct control. For example, we can manage the certificate (the file used to verify identity and provide context on establishing encrypted connections) between clients and Cloudflare because it’s our job in that connection to provide it to clients, but when talking to origin servers, Cloudflare is the client.

Customers need to acquire and provision an origin certificate on their host. They then have to configure Cloudflare to expect the new certificate from the origin when opening a connection. Needing to manually configure connection security across multiple different places requires effort and is prone to human error.

This issue was discussed in the original Universal SSL blog:

For a site that did not have SSL before, we will default to our Flexible SSL mode, which means traffic from browsers to Cloudflare will be encrypted, but traffic from Cloudflare to a site’s origin server will not. We strongly recommend site owners install a certificate on their web servers so we can encrypt traffic to the origin … Once you’ve installed a certificate on your web server, you can enable the Full or Strict SSL modes which encrypt origin traffic and provide a higher level of security.

Over the years Cloudflare has introduced numerous products to help customers configure how Cloudflare should talk to their origin. These products include a certificate authority to help customers obtain a certificate to verify their origin server’s identity and encryption capabilities, Authenticated Origin Pulls that ensures only HTTPS (encrypted) requests from Cloudflare will receive a response from the origin server, and Cloudflare Tunnels that can be configured to proactively establish secure and private tunnels to the nearest Cloudflare data center. Additionally, the ACME protocol and its corresponding Certbot tooling make it easier than ever to obtain and manage publicly-trusted certificates on customer origins. While these technologies help customers configure how Cloudflare should communicate with their origin server, they still require manual configuration changes on the origin and to Cloudflare settings.

Ensuring certificates are configured appropriately on origin servers and informing Cloudflare about how we should communicate with origins can be anxiety-inducing because misconfiguration can lead to downtime if something isn’t deployed or configured correctly.

To simplify this process and help identify the most secure options that customers could be using without any misconfiguration risk, Cloudflare introduced the SSL/TLS Recommender in 2021. The Recommender works by probing customer origins with different SSL/TLS settings to provide a recommendation whether the SSL/TLS encryption mode for the web property can be improved. The Recommender has been in production for three years and has consistently managed to provide high quality origin-security recommendations for Cloudflare’s customers.

The SSL/TLS Recommender system serves as the brain of the automatic origin connection service that we are announcing today.

How does SSL/TLS Recommendation work?

The Recommender works by actively comparing content on web pages that have been downloaded using different SSL/TLS modes to see if it is safe and risk-free to update the mode Cloudflare uses to connect to origin servers.

Cloudflare currently offers five SSL/TLS modes:

  1. Off: No encryption is used for traffic between browsers and Cloudflare or between Cloudflare and origins. Everything is cleartext HTTP.
  2. Flexible: Traffic from browsers to Cloudflare can be encrypted via HTTPS, but traffic from Cloudflare to the origin server is not. This mode is common for origins that do not support TLS, though upgrading the origin configuration is recommended whenever possible. A guide for upgrading is available here.
  3. Full: Cloudflare matches the browser request protocol when connecting to the origin. If the browser uses HTTP, Cloudflare connects to the origin via HTTP; if HTTPS, Cloudflare uses HTTPS without validating the origin’s certificate. This mode is common for origins that use self-signed or otherwise invalid certificates.
  4. Full (Strict): Similar to Full Mode, but with added validation of the origin server’s certificate, which can be issued by a public CA like Let’s Encrypt or by Cloudflare Origin CA.
  5. Strict (SSL-only origin pull): Regardless of whether the browser-to-Cloudflare connection uses HTTP or HTTPS, Cloudflare always connects to the origin over HTTPS with certificate validation.

HTTP from visitor

HTTPS from visitor

Off

HTTP to origin

HTTP to origin

Flexible

HTTP to origin

HTTP to origin

Full

HTTP to origin

HTTPS without cert validation to origin

Full (strict)

HTTP to origin

HTTPS with cert validation to origin

Strict (SSL-only origin pull)

HTTPS with cert validation to origin

HTTPS with cert validation to origin

The SSL/TLS Recommender works by crawling customer sites and collecting links on the page (like any web crawler). The Recommender downloads content over both HTTP and HTTPS, making GET requests to avoid modifying server resources. It then uses a content similarity algorithm, adapted from the research paper “A Deeper Look at Web Content Availability and Consistency over HTTP/S” (TMA Conference 2020), to determine if content matches. If the content does match, the Recommender makes a determination for whether the SSL/TLS mode can be increased without misconfiguration risk.

The recommendations are currently delivered to customers via email.

When the Recommender is making security recommendations, it errs on the side of maintaining current site functionality to avoid breakage and usability issues. If a website is non-functional, blocks all bots, or has SSL/TLS-specific Page Rules or Configuration Rules, the Recommender may not complete its scans and provide a recommendation. It was designed to maximize domain security, but will not help resolve website or domain functionality issues.

The crawler uses the user agent “Cloudflare-SSLDetector” and is included in Cloudflare’s list of known good bots. It ignores robots.txt (except for rules specifically targeting its user agent) to ensure accurate recommendations.

When downloading content from your origin server over both HTTP and HTTPS and comparing the content, the Recommender understands the current SSL/TLS encryption mode that your website uses and what risk there might be to the site functionality if the recommendation is followed.

Using SSL/TLS Recommender to automatically manage SSL/TLS settings

Previously, signing up for the SSL/TLS Recommender provided a good experience for customers, but only resulted in an email recommendation in the event that a zone’s current SSL/TLS modes could be updated. To Cloudflare, this was a positive signal that customers wanted their websites to have more secure connections to their origin servers – over 2 million domains have enabled the SSL/TLS Recommender. However, we found that a significant number of users would not complete the next step of pushing the button to inform Cloudflare that we could communicate over the upgraded settings. Only 30% of the recommendations that the system provided were followed.

With the system designed to increase security while avoiding any breaking changes, we wanted to provide an option for customers to allow the Recommender to help upgrade their site security, without requiring further manual action from the customer. Therefore, we are introducing a new option for managing SSL/TLS configuration on Cloudflare: Automatic SSL/TLS.

Automatic SSL/TLS uses the SSL/TLS Recommender to make the determination as to what encryption mode is the most secure and safest for a website to be set to. If there is a more secure option for your website (based on your origin certification or capabilities), Automatic SSL/TLS will find it and apply it for your domain. The other option, Custom SSL/TLS, will work exactly like the setting the encryption mode does today. If you know what setting you want, just select it using Custom SSL/TLS, and we’ll use it.

Automatic SSL/TLS is currently meant to service an entire website, which typically works well for those with a single origin. For those concerned that they have more complex setups which use multiple origin servers with different security capabilities, don’t worry. Automatic SSL/TLS will still avoid breaking site functionality by looking for the best setting that works for all origins serving a part of the site’s traffic.

If customers want to segment the SSL/TLS mode used to communicate with the numerous origins that service their domain, they can achieve this by using Configuration Rules. These rules allow you to set more precise modes that Cloudflare should respect (based on path or subdomain or even IP address) to maximize the security of the domain based on your desired Rules criteria. If your site uses SSL/TLS-specific settings in a Configuration Rule or Page rule, those settings will override the zone-wide Automatic and Custom settings.

The goal of Automatic SSL/TLS is to simplify and maximize the origin-facing security for customers on Cloudflare. We want this to be the new default for all websites on Cloudflare, but we understand that not everyone wants this new default, and we will respect your decision for how Cloudflare should communicate with your origin server. If you block the Recommender from completing its crawls, the origin server is non-functional or can’t be crawled, or if you want to opt out of this default and just continue using the same encryption mode you are using today, we will make it easy for you to tell us what you prefer.

How to onboard to Automatic SSL/TLS

To improve the security settings for everyone by default, we are making the following default changes to how Cloudflare configures the SSL/TLS level for all zones:

Starting on August 8, 2024, websites with the SSL/TLS Recommender currently enabled will have the Automatic SSL/TLS setting enabled by default. Enabling does not mean that the Recommender will begin scanning and applying new settings immediately though. There will be a one-month grace period before the first scans begin and the recommended settings are applied. Enterprise (ENT) customers will get a six-week grace period. Origin scans will start getting scheduled by September 9, 2024, for non-Enterprise customers and September 23rd for ENT customers with the SSL Recommender enabled. This will give customers the ability to opt out by removing Automatic SSL/TLS and selecting the Custom mode that they want to use instead.

Further, during the second week of September all new zones signing up for Cloudflare will start seeing the Automatic SSL/TLS setting enabled by default.

Beginning September 16, 2024, remaining Free and Pro customers will start to see the new Automatic SSL/TLS setting. They will also have a one-month grace period to opt out before the scans start taking effect.

Customers in the cohort having the new Automatic SSL/TLS setting applied will receive an email communication regarding the date that they are slated for this migration as well as a banner on the dashboard that mentions this transition as well. If they do not wish for Cloudflare to change anything in their configurations, the process for opt-out of this migration is outlined below.

Following the successful migration of Free and Pro customers, we will proceed to Business and Enterprise customers with a similar cadence. These customers will get email notifications and information in the dashboard when they are in the migration cohort.

The Automatic SSL/TLS setting will not impact users that are already in Strict or Full (strict) mode nor will it impact websites that have opted-out.

Opting out

There are a number of reasons why someone might want to configure a lower-than-optimal security setting for their website. Some may want to set a lower security setting for testing purposes or to debug some behavior. Whatever the reason, the options to opt-out of the Automatic SSL/TLS setting during the migration process are available in the dashboard and API.

To opt-out, simply select Custom SSL/TLS in the dashboard (instead of the enabled Automatic SSL/TLS) and we will continue to use the previously set encryption mode that you were using prior to the migration. Automatic and Custom SSL/TLS modes can be found in the Overview tab of the SSL/TLS section of the dashboard. To enable your preferred mode, select configure.

If you want to opt out via the API you can make this API call on or before the grace period expiration date.

    curl --request PATCH \
        --url https://api.cloudflare.com/client/v4/zones/<insert_zone_tag_here>/settings/ssl_automatic_mode \
        --header 'Authorization: Bearer <insert_api_token_here>' \
        --header 'Content-Type: application/json' \
        --data '{"value":"custom"}'

If an opt-out is triggered, there will not be a change to the currently configured SSL/TLS setting. You are also able to change the security level at any time by going to the SSL/TLS section of the dashboard and choosing the Custom setting you want (similar to how this is accomplished today).

If at a later point you’d like to opt in to Automatic SSL/TLS, that option is available by changing your setting from Custom to Automatic.

What if I want to be more secure now?

We will begin to roll out this change to customers with the SSL/TLS Recommender enabled on August 8, 2024. If you want to enroll in that group, we recommend enabling the Recommender as soon as possible.

If you read this and want to make sure you’re at the highest level of backend security already, we recommend Full (strict) or Strict mode. Directions on how to make sure you’re correctly configured in either of those settings are available here and here.

If you prefer to wait for us to automatically upgrade your connection to the maximum encryption mode your origin supports, please watch your inbox for the date we will begin rolling out this change for you.

Avoiding downtime: modern alternatives to outdated certificate pinning practices

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/why-certificate-pinning-is-outdated


In today’s world, technology is quickly evolving and some practices that were once considered the gold standard are quickly becoming outdated. At Cloudflare, we stay close to industry changes to ensure that we can provide the best solutions to our customers. One practice that we’re continuing to see in use that no longer serves its original purpose is certificate pinning. In this post, we’ll dive into certificate pinning, the consequences of using it in today’s Public Key Infrastructure (PKI) world, and alternatives to pinning that offer the same level of security without the management overhead.  

PKI exists to help issue and manage TLS certificates, which are vital to keeping the Internet secure – they ensure that users access the correct applications or servers and that data between two parties stays encrypted. The mis-issuance of a certificate can pose great risk. For example, if a malicious party is able to issue a TLS certificate for your bank’s website, then they can potentially impersonate your bank and intercept that traffic to get access to your bank account. To prevent a mis-issued certificate from intercepting traffic, the server can give a certificate to the client and say “only trust connections if you see this certificate and drop any responses that present a different certificate” – this practice is called certificate pinning.

In the early 2000s, it was common for banks and other organizations that handle sensitive data to pin certificates to clients. However, over the last 20 years, TLS certificate issuance has evolved and changed, and new solutions have been developed to help customers achieve the security benefit they receive through certificate pinning, with simpler management, and without the risk of disruption.

Cloudflare’s mission is to help build a better Internet, which is why our teams are always focused on keeping domains secure and online.

Why certificate pinning is causing more outages now than it did before

Certificate pinning is not a new practice, so why are we emphasizing the need to stop using it now? The reason is that the PKI ecosystem is moving towards becoming more agile, flexible, and secure. As a part of this change, certificate authorities (CAs) are starting to rotate certificates and their intermediates, certificates that bridge the root certificate and the domain certificate, more frequently to improve security and encourage automation.

These more frequent certificate rotations are problematic from a pinning perspective because certificate pinning relies on the exact matching of certificates. When a certificate is rotated, the new certificate might not match the pinned certificate on the client side. If the pinned certificate is not updated to reflect the contents of the rotated certificate, the client will reject the new certificate, even if it’s valid and issued by the same CA. This mismatch leads to a failure in establishing a secure connection, causing the domain or application to become inaccessible until the pinned certificate is updated.

Since the start of 2024, we have seen the number of customer reported outages caused by certificate pinning significantly increase. (As of this writing, we are part way through July and Q3 has already seen as many outages as the last three quarters of 2023 combined.)

We can attribute this rise to two major events: Cloudflare migrating away from using DigiCert as a certificate authority and Google and Let’s Encrypt intermediate CA rotations.

Before migrating customer’s certificates away from using DigiCert as the CA, Cloudflare sent multiple notifications to customers to inform them that they should update or remove their certificate pins, so that the migration does not impact their domain’s availability.

However, what we’ve learned is that almost all customers that were impacted by the change were unaware that they had a certificate pin in place. One of the consequences of using certificate pinning is that the “set and forget” mentality doesn’t work, now that certificates are being rotated more frequently. Instead, changes need to be closely monitored to ensure that a regular certificate renewal doesn’t cause an outage. This goes to show that to implement certificate pinning successfully, customers need a robust system in place to track certificate changes and implement them.

We built our Universal SSL pipeline to be resilient and redundant, ensuring that we can always issue and renew a TLS certificate on behalf of our customers, even in the event of a compromise or revocation. CAs are starting to make changes like more frequent certificate rotations to encourage a move towards a more secure ecosystem. Now, it’s up to domain owners to stop implementing legacy practices like certificate pinning, which cause breaking changes, and instead start adopting modern standards that aim to provide the same level of security, but without the management overhead or risk.

Modern standards & practices are making the need for certificate pinning obsolete

Shorter certificate lifetimes

Over the last few years, we have seen certificate lifetimes quickly decrease. Before 2011, a certificate could be valid for up to 96 months (eight years) and now, in 2024, the maximum validity period for a certificate is 1 year. We’re seeing this trend continue to develop, with Google Chrome pushing for shorter CA, intermediate, and certificate lifetimes, advocating for 3 month certificate validity as the new standard.

This push improves security and redundancy of the entire PKI ecosystem in several ways. First, it reduces the scope of a compromise by limiting the amount of time that a malicious party could control a TLS certificate or private key. Second, it reduces reliance on certificate revocation, a process that lacks standardization and enforcement by clients, browsers, and CAs. Lastly, it encourages automation as a replacement for legacy certificate practices that are time-consuming and error-prone.

Cloudflare is moving towards only using CAs that follow the ACME (Automated Certificate Management Environment) protocol, which by default, issues certificates with 90 day validity periods. We have already started to roll this out to Universal SSL certificates and have removed the ability to issue 1-year certificates as a part of our reduced usage of DigiCert.

Regular rotation of intermediate certificates

The CAs that Cloudflare partners with, Let’s Encrypt and Google Trust Services, are starting to rotate their intermediate CAs more frequently. This increased rotation is beneficial from a security perspective because it limits the lifespan of intermediate certificates, reducing the window of opportunity for attackers to exploit a compromised intermediate. Additionally, regular rotations make it easier to revoke an intermediate certificate if it becomes compromised, enhancing the overall security and resiliency of the PKI ecosystem.

Both Let’s Encrypt and Google Trust Services changed their intermediate chains in June 2024. In addition, Let’s Encrypt has started to balance their certificate issuance across 10 intermediates (5 RSA and 5 ECDSA).

Cloudflare customers using Advanced Certificate Manager have the ability to choose their issuing CA. The issue is that even if Cloudflare uses the same CA for a certificate renewal, there is no guarantee that the same certificate chain (root or intermediate) will be used to issue the renewed certificate. As a result, if pinning is used, a successful renewal could cause a full outage for a domain or application.

This happens because certificate pinning relies on the exact matching of certificates. When an intermediate certificate is rotated or changed, the new certificate might not match the pinned certificate on the client side. As a result, the client will reject the renewed certificate, even if it’s a valid certificate issued by the same CA. This mismatch leads to a failure on the client side, causing the domain to become inaccessible until the pinned certificate is updated to reflect the new intermediate certificate. This risk of an unexpected outage is a major downside of continuing to use certificate pinning, especially as CAs increasingly update their intermediates as a security measure.

Increased use of certificate transparency

Certificate transparency (CT) logs provide a standardized framework for monitoring and auditing the issuance of TLS certificates. CT logs help detect misissued or malicious certificates and Cloudflare customers can set up CT monitoring to receive notifications about any certificates issued for their domain. This provides a better mechanism for detecting certificate mis-issuance, reducing the need for pinning.

Why modern standards make certificate pinning obsolete

Together, these practices – shorter certificate lifetimes, regular rotations of intermediate certificates, and increased use of certificate transparency – address the core security concerns that certificate pinning was initially designed to mitigate. Shorter lifetimes and frequent rotations limit the impact of compromised certificates, while certificate transparency allows for real time monitoring and detection of misissued certificates. These advancements are automated, scalable, and robust and eliminate the need for the manual and error-prone process of certificate pinning. By adopting these modern standards, organizations can achieve a higher level of security and resiliency without the management overhead and risk associated with certificate pinning.

Reasons behind continued use of certificate pinning

Originally, certificate pinning was designed to prevent monster-in-the-middle (MITM) attacks by associating a hostname with a specific TLS certificate, ensuring that a client could only access an application if the server presented a certificate issued by the domain owner.

Certificate pinning was traditionally used to secure IoT (Internet of Things) devices, mobile applications, and APIs. IoT devices are usually equipped with more limited processing power and are oftentimes unable to perform software updates. As a result, they’re less likely to perform things like certificate revocation checks to ensure that they’re using a valid certificate. As a result, it’s common for these devices to come pre-installed with a set of trusted certificate pins to ensure that they can maintain a high level of security. However, the increased frequency of certificate changes poses significant risk, as many devices have immutable software, preventing timely updates to certificate pins during renewals.

Similarly, certificate pinning has been employed to secure Android and iOS applications, ensuring that only the correct certificates are served. Despite this, both Apple and Google warn developers against the use of certificate pinning due to the potential for failures if not implemented correctly.

Understanding the trade-offs of different certificate pinning implementations

While certificate pinning can be applied at various levels of the certificate chain, offering different levels of granularity and security, we don’t recommend it due to the challenges and risks associated with its use.

Pinning certificates at the root certificate

Pinning the root certificate instructs a client to only trust certificates issued by that specific Certificate Authority (CA).

Advantages:

  • Simplified management: Since root certificates have long lifetimes (>10 years) and rarely change, pinning at the root reduces the need to frequently update certificate pins, making this the easiest option in terms of management overhead.

Disadvantages:

  • Broader trust: Most Certificate Authorities (CAs) issue their certificates from one root, so pinning a root CA certificate enables the client to trust every certificate issued from that CA. However, this broader trust can be problematic. If the root CA is compromised, every certificate issued by that CA is also compromised, which significantly increases the potential scope and impact of a security breach. This broad trust can therefore create a single point of failure, making the entire ecosystem more vulnerable to attacks.
  • Neglected Maintenance: Root certificates are infrequently rotated, which can lead to a “set and forget” mentality when pinning them. Although it’s rare, CAs do change their roots and when this happens, a correctly renewed certificate will break the pin, causing an outage. Since these pins are rarely updated, resolving such outages can be time-consuming as engineering teams try to identify and locate where the outdated pins have been set.

Pinning certificates at the intermediate certificate

Pinning an intermediate certificate instructs a client to only trust certificates issued by a specific intermediate CA, issued from a trusted root CA. With lifetimes ranging from 3 to 10 years, intermediate certificates offer a better balance between security and flexibility.

Advantages:

  • Better security: Narrows down the trust to certificates issued by a specific intermediate CA.
  • Simpler management: With intermediate CA lifetimes spanning a few years, certificate pins require less frequent updates, reducing the maintenance burden.

Disadvantages:

  • Broad trust: While pinning on an intermediate certificate is more restrictive than pinning on a root certificate, it still allows for a broad range of certificates to be trusted.
  • Maintenance: Intermediate certificates are rotated more frequently than root certificates, requiring more regular updates to pinned certificates.
  • Less predictability: With CAs like Let’s Encrypt issuing their certificates from varying intermediates, it’s no longer possible to predict which certificate chain will be used during a renewal, making it more likely for a certificate renewal to break a certificate pin and cause an outage.

Pinning certificates at the leaf certificate

Pinning the leaf certificate instructs a client to only trust that specific certificate. Although this option offers the highest level of security, it also poses the greatest risk of causing an outage during a certificate renewal.

Advantages:

  • High security: Provides the highest level of security by ensuring that only a specific certificate is trusted, minimizing the risk of a monster-in-the-middle attack.

Disadvantages:

  • Risky: Requires careful management of certificate renewals to prevent outages.
  • Management burden: Leaf certificates have shorter lifetimes, with 90 days becoming the standard, requiring constant updates to the certificate pin to avoid a breaking change during a renewal.

Alternatives to certificate pinning

Given the risks and challenges associated with certificate pinning, we recommend the following as more effective and modern alternatives to achieve the same level of security (preventing a mis-issued certificate from intercepting traffic) that certificate pinning aims to provide.

Shorter certificate lifetimes

Using shorter certificate lifetimes ensures that certificates are regularly renewed and replaced, reducing the risk of misuse of a compromised certificate by limiting the window of opportunity for attackers.

By default, Cloudflare issues 90-day certificates for customers. Customers using Advanced Certificate Manager can request TLS certificates with lifetimes as short as 14 days.

CAA records to restrict which CAs can issue certificates for a domain

Certification Authority Authorization (CAA) DNS records allow domain owners to specify which CAs are allowed to issue certificates for their domain. This adds an extra layer of security by restricting issuance to trusted authorities, providing a similar benefit as pinning a root CA certificate. For example, if you’re using Google Trust Services as your CA, you can add the following CAA DNS record to ensure that only that CA issues certificates for your domain: 

example.com         CAA 0 issue "pki.goog"

By default, Cloudflare sets CAA records on behalf of customers to ensure that certificates can be issued from the CAs that Cloudflare partners with. Customers can choose to further restrict that list of CAs by adding their own CAA records.

Certificate Transparency & monitoring

Certificate Transparency (CT) provides the ability to monitor and audit certificate issuances. By logging certificates in publicly accessible CT logs, organizations are able to monitor, detect, and respond to misissued certificates at the time they are issued.

Cloudflare customers can set up CT Monitoring to receive notifications when certificates are issued in their domain. Today, we notify customers using the product about all certificates issued for their domains. In the future, we will allow customers to filter those notifications, so that they are only notified when an external party that isn’t Cloudflare issues a certificate for the owner’s domain. This product is available to all customers and can be enabled with the click of a button.

Multi-vantage point Domain Control Validation (DCV) checks to prevent mis-issuances

For a CA to issue a certificate, the domain owner needs to prove ownership of the domain by serving Domain Control Validation (DCV) records. While uncommon, one attack vector of DCV validation allows an actor to perform BGP hijacking to spoof the DNS response and trick a CA into mis-issuing a certificate. To prevent this form of attack, CAs have started to perform DCV validation checks from multiple locations to ensure that a certificate is only issued when a full quorum is met.

Cloudflare has developed its own solution that CAs can use to perform multi vantage point DCV checks. In addition, Cloudflare partners with CAs like Let’s Encrypt who continue to develop these checks to support new locations, reducing the risk of a certificate mis-issuance.

Specifying ACME account URI in CAA records

A new enhancement to the ACME protocol allows certificate requesting parties to specify an ACME account URI, the ID of the ACME account that will be requesting the certificates, in CAA records to tighten control over the certificate issuance process. This ensures that only certificates issued through an authorized ACME account are trusted, adding another layer of verification to certificate issuance. Let’s Encrypt supports this extension to CAA records which allows users with a Let’s Encrypt certificate to set a CAA DNS record, such as the following: 

example.com         CAA 0 issue "letsencrypt.org;accounturi=https://acme-v02.api.letsencrypt.org/acme/acct/<account_id>"

With this record, Let’s Encrypt subscribers can ensure that only Let’s Encrypt can issue certificates for their domain and that these certificates were only issued through their ACME account.

Cloudflare will look to support this enhancement automatically for customers in the future.

Conclusion

Years ago, certificate pinning was a valuable tool for enhancing security, but over the last 20 years, it has failed to keep up with new advancements in the certificate ecosystem. As a result, instead of providing the intended security benefit, it has increased the number of outages caused during a successful certificate renewal. With new enhancements in certificate issuance standards and certificate transparency, we’re encouraging our customers and the industry to move towards adopting those new standards and deprecating old ones.

If you’re a Cloudflare customer and are required to pin your certificate, the only way to ensure a zero-downtime renewal is to upload your own custom certificates. We recommend using the staging network to test your certificate renewal to ensure you have updated your certificate pin.

How we ensure Cloudflare customers aren’t affected by Let’s Encrypt’s certificate chain change

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/shortening-lets-encrypt-change-of-trust-no-impact-to-cloudflare-customers


Let’s Encrypt, a publicly trusted certificate authority (CA) that Cloudflare uses to issue TLS certificates, has been relying on two distinct certificate chains. One is cross-signed with IdenTrust, a globally trusted CA that has been around since 2000, and the other is Let’s Encrypt’s own root CA, ISRG Root X1. Since Let’s Encrypt launched, ISRG Root X1 has been steadily gaining its own device compatibility.

On September 30, 2024, Let’s Encrypt’s certificate chain cross-signed with IdenTrust will expire. After the cross-sign expires, servers will no longer be able to serve certificates signed by the cross-signed chain. Instead, all Let’s Encrypt certificates will use the ISRG Root X1 CA.

Most devices and browser versions released after 2016 will not experience any issues as a result of the change since the ISRG Root X1 will already be installed in those clients’ trust stores. That’s because these modern browsers and operating systems were built to be agile and flexible, with upgradeable trust stores that can be updated to include new certificate authorities.

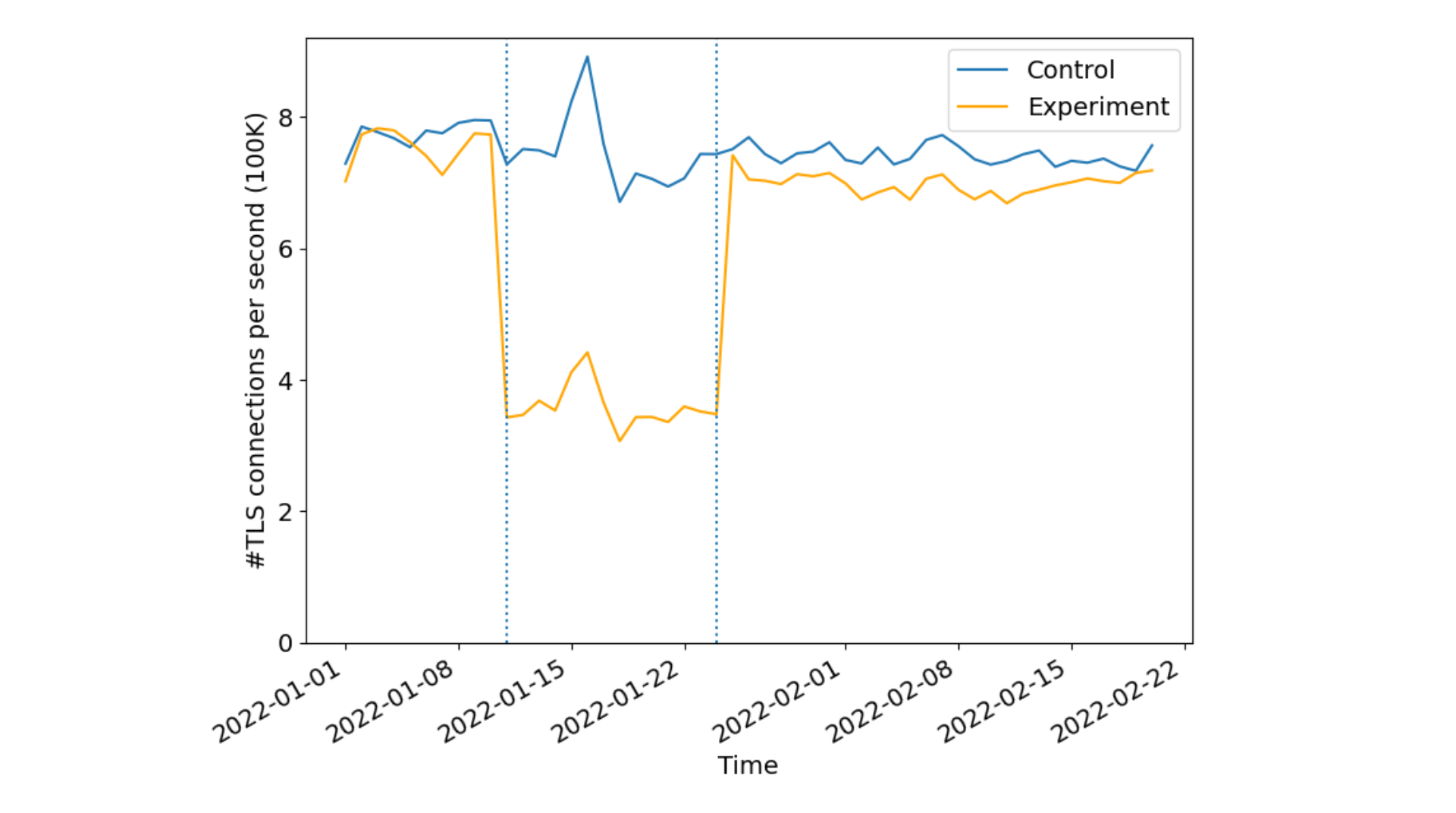
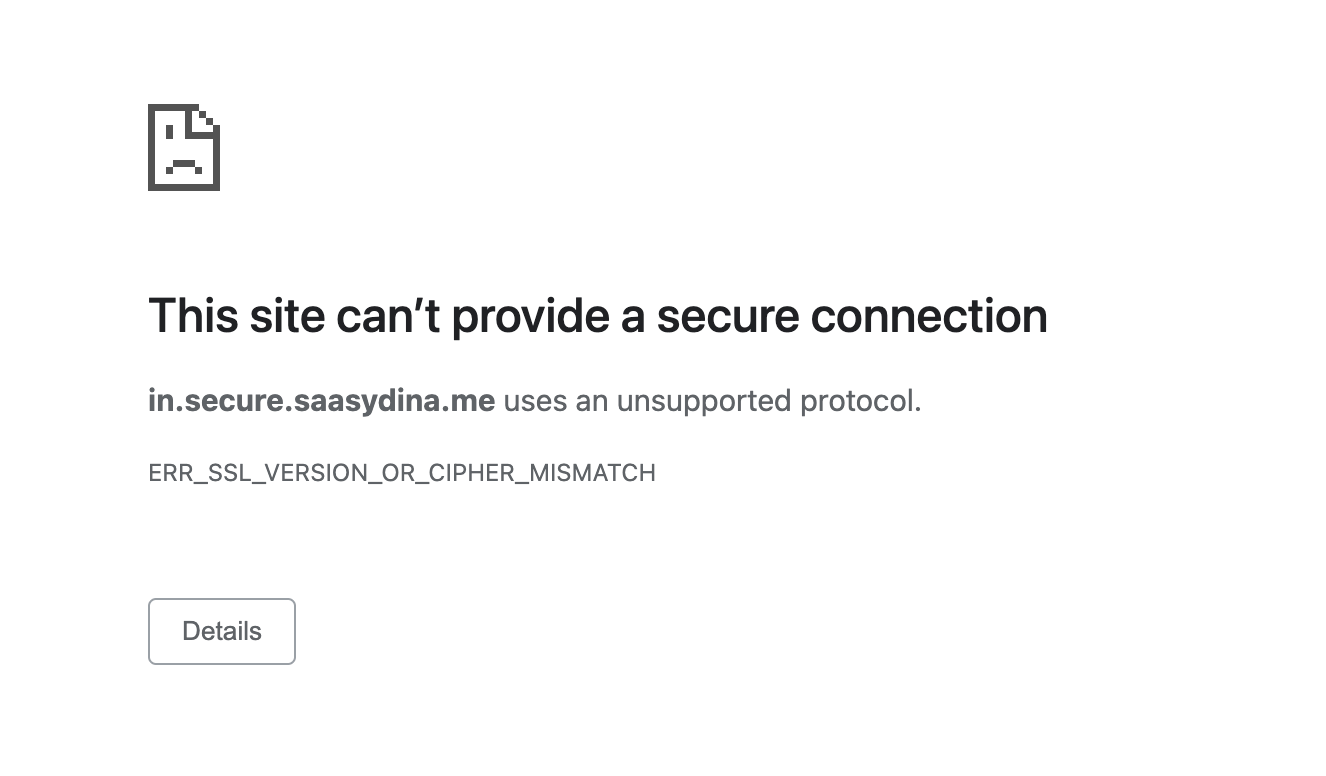
The change in the certificate chain will impact legacy devices and systems, such as devices running Android version 7.1.1 (released in 2016) or older, as those exclusively rely on the cross-signed chain and lack the ISRG X1 root in their trust store. These clients will encounter TLS errors or warnings when accessing domains secured by a Let’s Encrypt certificate. We took a look at the data ourselves and found that, of all Android requests, 2.96% of them come from devices that will be affected by the change. That’s a substantial portion of traffic that will lose access to the Internet. We’re committed to keeping those users online and will modify our certificate pipeline so that we can continue to serve users on older devices without requiring any manual modifications from our customers.

A better Internet, for everyone

In the past, we invested in efforts like “No Browsers Left Behind” to help ensure that we could continue to support clients as SHA-1 based algorithms were being deprecated. Now, we’re applying the same approach for the upcoming Let’s Encrypt change.

We have made the decision to remove Let’s Encrypt as a certificate authority from all flows where Cloudflare dictates the CA, impacting Universal SSL customers and those using SSL for SaaS with the “default CA” choice.

Starting in June 2024, one certificate lifecycle (90 days) before the cross-sign chain expires, we’ll begin migrating Let’s Encrypt certificates that are up for renewal to use a different CA, one that ensures compatibility with older devices affected by the change. That means that going forward, customers will only receive Let’s Encrypt certificates if they explicitly request Let’s Encrypt as the CA.

The change that Let’s Encrypt is making is a necessary one. For us to move forward in supporting new standards and protocols, we need to make the Public Key Infrastructure (PKI) ecosystem more agile. By retiring the cross-signed chain, Let’s Encrypt is pushing devices, browsers, and clients to support adaptable trust stores.

However, we’ve observed changes like this in the past and while they push the adoption of new standards, they disproportionately impact users in economically disadvantaged regions, where access to new technology is limited.

Our mission is to help build a better Internet and that means supporting users worldwide. We previously published a blog post about the Let’s Encrypt change, asking customers to switch their certificate authority if they expected any impact. However, determining the impact of the change is challenging. Error rates due to trust store incompatibility are primarily logged on clients, reducing the visibility that domain owners have. In addition, while there might be no requests incoming from incompatible devices today, it doesn’t guarantee uninterrupted access for a user tomorrow.

Cloudflare’s certificate pipeline has evolved over the years to be resilient and flexible, allowing us to seamlessly adapt to changes like this without any negative impact to our customers.  

How Cloudflare has built a robust TLS certificate pipeline

Today, Cloudflare manages tens of millions of certificates on behalf of customers. For us, a successful pipeline means:

  1. Customers can always obtain a TLS certificate for their domain
  2. CA related issues have zero impact on our customer’s ability to obtain a certificate
  3. The best security practices and modern standards are utilized
  4. Optimizing for future scale
  5. Supporting a wide range of clients and devices

Every year, we introduce new optimizations into our certificate pipeline to maintain the highest level of service. Here’s how we do it…

Ensuring customers can always obtain a TLS certificate for their domain

Since the launch of Universal SSL in 2014, Cloudflare has been responsible for issuing and serving a TLS certificate for every domain that’s protected by our network. That might seem trivial, but there are a few steps that have to successfully execute in order for a domain to receive a certificate:

  1. Domain owners need to complete Domain Control Validation for every certificate issuance and renewal.
  2. The certificate authority needs to verify the Domain Control Validation tokens to issue the certificate.
  3. CAA records, which dictate which CAs can be used for a domain, need to be checked to ensure only authorized parties can issue the certificate.
  4. The certificate authority must be available to issue the certificate.

Each of these steps requires coordination across a number of parties — domain owners, CDNs, and certificate authorities. At Cloudflare, we like to be in control when it comes to the success of our platform. That’s why we make it our job to ensure each of these steps can be successfully completed.

We ensure that every certificate issuance and renewal requires minimal effort from our customers. To get a certificate, a domain owner has to complete Domain Control Validation (DCV) to prove that it does in fact own the domain. Once the certificate request is initiated, the CA will return DCV tokens which the domain owner will need to place in a DNS record or an HTTP token. If you’re using Cloudflare as your DNS provider, Cloudflare completes DCV on your behalf by automatically placing the TXT token returned from the CA into your DNS records. Alternatively, if you use an external DNS provider, we offer the option to Delegate DCV to Cloudflare for automatic renewals without any customer intervention.

Once DCV tokens are placed, Certificate Authorities (CAs) verify them. CAs conduct this verification from multiple vantage points to prevent spoofing attempts. However, since these checks are done from multiple countries and ASNs (Autonomous Systems), they may trigger a Cloudflare WAF rule which can cause the DCV check to get blocked. We made sure to update our WAF and security engine to recognize that these requests are coming from a CA to ensure they’re never blocked so DCV can be successfully completed.

Some customers have CA preferences, due to internal requirements or compliance regulations. To prevent an unauthorized CA from issuing a certificate for a domain, the domain owner can create a Certification Authority Authorization (CAA) DNS record, specifying which CAs are allowed to issue a certificate for that domain. To ensure that customers can always obtain a certificate, we check the CAA records before requesting a certificate to know which CAs we should use. If the CAA records block all of the CAs that are available in Cloudflare’s pipeline and the customer has not uploaded a certificate from the CA of their choice, then we add CAA records on our customers’ behalf to ensure that they can get a certificate issued. Where we can, we optimize for preference. Otherwise, it’s our job to prevent an outage by ensuring that there’s always a TLS certificate available for the domain, even if it does not come from a preferred CA.

Today, Cloudflare is not a publicly trusted certificate authority, so we rely on the CAs that we use to be highly available. But, 100% uptime is an unrealistic expectation. Instead, our pipeline needs to be prepared in case our CAs become unavailable.

Ensuring that CA-related issues have zero impact on our customer’s ability to obtain a certificate

At Cloudflare, we like to think ahead, which means preventing incidents before they happen. It’s not uncommon for CAs to become unavailable — sometimes this happens because of an outage, but more commonly, CAs have maintenance periods every so often where they become unavailable for some period of time.

It’s our job to ensure CA redundancy, which is why we always have multiple CAs ready to issue a certificate, ensuring high availability at all times. If you’ve noticed different CAs issuing your Universal SSL certificates, that’s intentional. We evenly distribute the load across our CAs to avoid any single point of failure. Plus, we keep a close eye on latency and error rates to detect any issues and automatically switch to a different CA that’s available and performant. You may not know this, but one of our CAs has around 4 scheduled maintenance periods every month. When this happens, our automated systems kick in seamlessly, keeping everything running smoothly. This works so well that our internal teams don’t get paged anymore because everything just works.

Adopting best security practices and modern standards  

Security has always been, and will continue to be, Cloudflare’s top priority, and so maintaining the highest security standards to safeguard our customer’s data and private keys is crucial.

Over the past decade, the CA/Browser Forum has advocated for reducing certificate lifetimes from 5 years to 90 days as the industry norm. This shift helps minimize the risk of a key compromise. When certificates are renewed every 90 days, their private keys remain valid for only that period, reducing the window of time that a bad actor can make use of the compromised material.

We fully embrace this change and have made 90 days the default certificate validity period. This enhances our security posture by ensuring regular key rotations, and has pushed us to develop tools like DCV Delegation that promote automation around frequent certificate renewals, without the added overhead. It’s what enables us to offer certificates with validity periods as low as two weeks, for customers that want to rotate their private keys at a high frequency without any concern that it will lead to certificate renewal failures.

Cloudflare has always been at the forefront of new protocols and standards. It’s no secret that when we support a new protocol, adoption skyrockets. This month, we will be adding ECDSA support for certificates issued from Google Trust Services. With ECDSA, you get the same level of security as RSA but with smaller keys. Smaller keys mean smaller certificates and less data passed around to establish a TLS connection, which results in quicker connections and faster loading times.

Optimizing for future scale

Today, Cloudflare issues almost 1 million certificates per day. With the recent shift towards shorter certificate lifetimes, we continue to improve our pipeline to be more robust. But even if our pipeline can handle the significant load, we still need to rely on our CAs to be able to scale with us. With every CA that we integrate, we instantly become one of their biggest consumers. We hold our CAs to high standards and push them to improve their infrastructure to scale. This doesn’t just benefit Cloudflare’s customers, but it helps the Internet by requiring CAs to handle higher volumes of issuance.

And now, with Let’s Encrypt shortening their chain of trust, we’re going to add an additional improvement to our pipeline — one that will ensure the best device compatibility for all.

Supporting all clients — legacy and modern

The upcoming Let’s Encrypt change will prevent legacy devices from making requests to domains or applications that are protected by a Let’s Encrypt certificate. We don’t want to cut off Internet access from any part of the world, which means that we’re going to continue to provide the best device compatibility to our customers, despite the change.

Because of all the recent enhancements, we are able to reduce our reliance on Let’s Encrypt without impacting the reliability or quality of service of our certificate pipeline. One certificate lifecycle (90 days) before the change, we are going to start shifting certificates to use a different CA, one that’s compatible with the devices that will be impacted. By doing this, we’ll mitigate any impact without any action required from our customers. The only customers that will continue to use Let’s Encrypt are ones that have specifically chosen Let’s Encrypt as the CA.

What to expect of the upcoming Let’s Encrypt change

Let’s Encrypt’s cross-signed chain will expire on September 30th, 2024. Although Let’s Encrypt plans to stop issuing certificates from this chain on June 6th, 2024, Cloudflare will continue to serve the cross-signed chain for all Let’s Encrypt certificates until September 9th, 2024.

90 days or one certificate lifecycle before the change, we are going to start shifting Let’s Encrypt certificates to use a different certificate authority. We’ll make this change for all products where Cloudflare is responsible for the CA selection, meaning this will be automatically done for customers using Universal SSL and SSL for SaaS with the “default CA” choice.

Any customers that have specifically chosen Let’s Encrypt as their CA will receive an email notification with a list of their Let’s Encrypt certificates and information on whether or not we’re seeing requests on those hostnames coming from legacy devices.

After September 9th, 2024, Cloudflare will serve all Let’s Encrypt certificates using the ISRG Root X1 chain. Here is what you should expect based on the certificate product that you’re using:

Universal SSL

With Universal SSL, Cloudflare chooses the CA that is used for the domain’s certificate. This gives us the power to choose the best certificate for our customers. If you are using Universal SSL, there are no changes for you to make to prepare for this change. Cloudflare will automatically shift your certificate to use a more compatible CA.

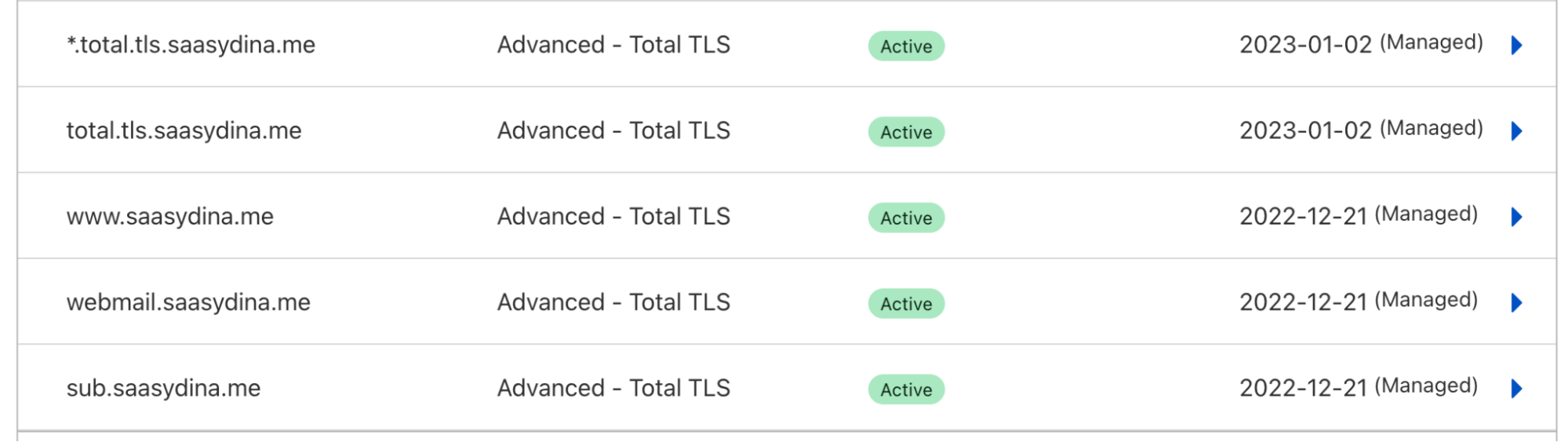
Advanced Certificates

With Advanced Certificate Manager, customers specifically choose which CA they want to use. If Let’s Encrypt was specifically chosen as the CA for a certificate, we will respect the choice, because customers may have specifically chosen this CA due to internal requirements, or because they have implemented certificate pinning, which we highly discourage.

If we see that a domain using an Advanced certificate issued from Let’s Encrypt will be impacted by the change, then we will send out email notifications to inform those customers which certificates are using Let’s Encrypt as their CA and whether or not those domains are receiving requests from clients that will be impacted by the change. Customers will be responsible for changing the CA to another provider, if they chose to do so.

SSL for SaaS

With SSL for SaaS, customers have two options: using a default CA, meaning Cloudflare will choose the issuing authority, or specifying which CA to use.

If you’re leaving the CA choice up to Cloudflare, then we will automatically use a CA with higher device compatibility.

If you’re specifying a certain CA for your custom hostnames, then we will respect that choice. We will send an email out to SaaS providers and platforms to inform them which custom hostnames are receiving requests from legacy devices. Customers will be responsible for changing the CA to another provider, if they chose to do so.

Custom Certificates

If you directly integrate with Let’s Encrypt and use Custom Certificates to upload your Let’s Encrypt certs to Cloudflare then your certificates will be bundled with the cross-signed chain, as long as you choose the bundle method “compatible” or “modern” and upload those certificates before September 9th, 2024. After September 9th, we will bundle all Let’s Encrypt certificates with the ISRG Root X1 chain. With the “user-defined” bundle method, we always serve the chain that’s uploaded to Cloudflare. If you upload Let’s Encrypt certificates using this method, you will need to ensure that certificates uploaded after September 30th, 2024, the date of the CA expiration, contain the right certificate chain.

In addition, if you control the clients that are connecting to your application, we recommend updating the trust store to include the ISRG Root X1. If you use certificate pinning, remove or update your pin. In general, we discourage all customers from pinning their certificates, as this usually leads to issues during certificate renewals or CA changes.

Conclusion

Internet standards will continue to evolve and improve. As we support and embrace those changes, we also need to recognize that it’s our responsibility to keep users online and to maintain Internet access in the parts of the world where new technology is not readily available. By using Cloudflare, you always have the option to choose the setup that’s best for your application.

For additional information regarding the change, please refer to our developer documentation.

Upcoming Let’s Encrypt certificate chain change and impact for Cloudflare customers

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/upcoming-lets-encrypt-certificate-chain-change-and-impact-for-cloudflare-customers


Let’s Encrypt, a publicly trusted certificate authority (CA) that Cloudflare uses to issue TLS certificates, has been relying on two distinct certificate chains. One is cross-signed with IdenTrust, a globally trusted CA that has been around since 2000, and the other is Let’s Encrypt’s own root CA, ISRG Root X1. Since Let’s Encrypt launched, ISRG Root X1 has been steadily gaining its own device compatibility.

On September 30, 2024, Let’s Encrypt’s certificate chain cross-signed with IdenTrust will expire. To proactively prepare for this change, on May 15, 2024, Cloudflare will stop issuing certificates from the cross-signed chain and will instead use Let’s Encrypt’s ISRG Root X1 chain for all future Let’s Encrypt certificates.

The change in the certificate chain will impact legacy devices and systems, such as Android devices version 7.1.1 or older, as those exclusively rely on the cross-signed chain and lack the ISRG X1 root in their trust store. These clients may encounter TLS errors or warnings when accessing domains secured by a Let’s Encrypt certificate.

According to Let’s Encrypt, more than 93.9% of Android devices already trust the ISRG Root X1 and this number is expected to increase in 2024, especially as Android releases version 14, which makes the Android trust store easily and automatically upgradable.

We took a look at the data ourselves and found that, from all Android requests, 2.96% of them come from devices that will be affected by the change. In addition, only 1.13% of all requests from Firefox come from affected versions, which means that most (98.87%) of the requests coming from Android versions that are using Firefox will not be impacted.

Preparing for the change

If you’re worried about the change impacting your clients, there are a few things that you can do to reduce the impact of the change. If you control the clients that are connecting to your application, we recommend updating the trust store to include the ISRG Root X1. If you use certificate pinning, remove or update your pin. In general, we discourage all customers from pinning their certificates, as this usually leads to issues during certificate renewals or CA changes.

If you experience issues with the Let’s Encrypt chain change, and you’re using Advanced Certificate Manager or SSL for SaaS on the Enterprise plan, you can choose to switch your certificate to use Google Trust Services as the certificate authority instead.

For more information, please refer to our developer documentation.

While this change will impact a very small portion of clients, we support the shift that Let’s Encrypt is making as it supports a more secure and agile Internet.

Embracing change to move towards a better Internet

Looking back, there were a number of challenges that slowed down the adoption of new technologies and standards that helped make the Internet faster, more secure, and more reliable.

For starters, before Cloudflare launched Universal SSL, free certificates were not attainable. Instead, domain owners had to pay around $100 to get a TLS certificate. For a small business, this is a big cost and without browsers enforcing TLS, this significantly hindered TLS adoption for years. Insecure algorithms have taken decades to deprecate due to lack of support of new algorithms in browsers or devices. We learned this lesson while deprecating SHA-1.

Supporting new security standards and protocols is vital for us to continue improving the Internet. Over the years, big and sometimes risky changes were made in order for us to move forward. The launch of Let’s Encrypt in 2015 was monumental. Let’s Encrypt allowed every domain to get a TLS certificate for free, which paved the way to a more secure Internet, with now around 98% of traffic using HTTPS.

In 2014, Cloudflare launched elliptic curve digital signature algorithm (ECDSA) support for Cloudflare-issued certificates and made the decision to issue ECDSA-only certificates to free customers. This boosted ECDSA adoption by pressing clients and web operators to make changes to support the new algorithm, which provided the same (if not better) security as RSA while also improving performance. In addition to that, modern browsers and operating systems are now being built in a way that allows them to constantly support new standards, so that they can deprecate old ones.

For us to move forward in supporting new standards and protocols, we need to make the Public Key Infrastructure (PKI) ecosystem more agile. By retiring the cross-signed chain, Let’s Encrypt is pushing devices, browsers, and clients to support adaptable trust stores. This allows clients to support new standards without causing a breaking change. It also lays the groundwork for new certificate authorities to emerge.

Today, one of the main reasons why there’s a limited number of CAs available is that it takes years for them to become widely trusted, that is, without cross-signing with another CA. In 2017, Google launched a new publicly trusted CA, Google Trust Services, that issued free TLS certificates. Even though they launched a few years after Let’s Encrypt, they faced the same challenges with device compatibility and adoption, which caused them to cross-sign with GlobalSign’s CA. We hope that, by the time GlobalSign’s CA comes up for expiration, almost all traffic is coming from a modern client and browser, meaning the change impact should be minimal.

AWS Certificate Manager will discontinue WHOIS lookup for email-validated certificates

Post Syndicated from Lerna Ekmekcioglu original https://aws.amazon.com/blogs/security/aws-certificate-manager-will-discontinue-whois-lookup-for-email-validated-certificates/

AWS Certificate Manager (ACM) is a managed service that you can use to provision, manage, and deploy public and private TLS certificates for use with Amazon Web Services (AWS) and your internal connected resources. Today, we’re announcing that ACM will be discontinuing the use of WHOIS lookup for validating domain ownership when you request email-validated TLS certificates.

WHOIS lookup is commonly used to query registration information for a given domain name. This information includes details such as when the domain was originally registered, and contact information for the domain owner and the technical and administrative contacts. Domain owners create and maintain domain registration information outside of ACM in WHOIS, which is a publicly available directory that contains information about domains sponsored by domain registrars and registries. You can use WHOIS lookup to view information about domains that are registered with Amazon Route 53.

Starting June 2024, ACM will no longer send domain validation emails by using WHOIS lookup for new email-validated certificates that you request. Starting October 2024, ACM will no longer send domain validation emails to mailboxes associated with WHOIS lookup for renewal of existing email-validated certificates. ACM will continue to send validation emails to the five common system addresses for the requested domain—we provide a list of these common system addresses in the next section of this post.

In this blog post, we share important details about this change and how you can prepare. Note that if you currently use DNS validation for your certificates requested from ACM, this change doesn’t affect you. These changes only apply to certificates that use email validation.

Background

When you request public certificates through ACM, you need to prove that you own or control the domain before ACM can issue the public certificate. ACM provides two options to validate ownership of a domain: DNS validation and email validation.

AWS recommends that you use DNS validation whenever possible so that ACM can automatically renew certificates that are requested from ACM without requiring action on your part. Email validation is another option that you can use to prove ownership of the domain, but you must manually validate ownership of the domain by using a link provided in an email. Figure 1 is a sample validation email from ACM for the AWS account 111122223333 and AWS US West (Oregon) Region (us-west-2) to validate ownership of the example.com domain.

Figure 1: Sample validation email for example.com domain

Figure 1: Sample validation email for example.com domain

How does ACM know where to send the validation email? Today, as part of the email validation process, ACM sends domain validation emails to the three contact addresses associated with the domain listed in the WHOIS database. These contact addresses are the domain registrant, technical contact, and administrative contact. You create and maintain domain registration information, including these contact addresses, outside of ACM—in the WHOIS database that your domain registrar provides.

Note: If you use Route53, see Updating contact information for a domain to update the contact information for your domain.

ACM also sends validation emails to the following five common system addresses for each domain: 

  • administrator@your_domain_name
  • hostmaster@your_domain_name
  • postmaster@your_domain_name
  • webmaster@your_domain_name
  • admin@your_domain_name

To prove that you own the domain, you must select the validation link included in these emails. ACM also sends validation emails to these same addresses to renew the certificate when the certificate is 45 days from expiry.

What’s changing?

If you currently use email validation for certificates requested from ACM, there are two important dates that you should be aware of:

  1. Starting June 2024, ACM will no longer send domain validation emails by using WHOIS lookup for new email-validated certificates that you request. ACM will continue to send validation emails to the three WHOIS lookup contact addresses for renewal of existing certificates, until October 2024.
  2. Starting October 2024, ACM will no longer send the validation emails to mailboxes associated with WHOIS lookup for existing certificates. After this date, ACM will not send validation emails to the three WHOIS lookup addresses for new or existing certificates.

ACM will continue to send validation emails to the five common system addresses that we listed in the previous section of this post.

Why are we making this change?

We’re making this change to mitigate a potential availability risk for ACM customers. A TLS certificate that ACM issues is valid for up to 395 days, and if you want to keep using it, you need to renew it prior to expiry. To renew an email-validated certificate, you must approve an email that ACM sends. ACM sends the first renewal email 45 days prior to certificate renewal, and if you don’t respond to this email, ACM sends additional reminders prior to expiry. If a certificate bound to one of your AWS resources—such as an Application Load Balancer—expires without being renewed, this could cause an outage for your application.

Some domain registrars that support WHOIS have made changes to the data that they publish to support their compliance with various privacy laws and recommended practices. Over the past several years, we’ve observed that the WHOIS lookup success rate has declined to less than 5 percent. If you rely on the contact addresses listed in the WHOIS database provided by your domain registrar to validate your domain ownership, this might create an availability risk. With a 5 percent success rate for WHOIS lookup, you might not receive validation emails for renewals of your certificates around 95 percent of the time. To provide a consistent mechanism for validating domain ownership when renewing certificates, ACM will only send validation emails to the five common system addresses that we listed in the Background section of this post.

What should you do to prepare?

If you currently monitor one of the five common system addresses (listed previously) for your domains, you don’t need to take any action. Otherwise, we strongly recommend that you create new DNS-validated certificates rather than creating and using email-validated certificates. ACM can automatically renew a DNS-validated certificate, without you taking any action, as long as the CNAME is accurately configured.

Alternatively, if you want to continue using email-validated certificates, we recommend that you monitor at least one of the five common email addresses listed previously. ACM sends the validation emails during certificate issuance for new ACM-issued certificates and during renewal of existing certificates. You can use the ACM describe-certificate API or check the certificate details on the ACM console to see if ACM previously sent validation emails to the relevant system addresses.

In addition, we strongly recommend that you use ACM Certificate Approaching Expiration events to monitor your certificates for expiry and help ensure that you’re notified about certificates that require an action from you to renew. For additional guidance, see How to manage certificate lifecycles using ACM event-driven workflows.

Conclusion

In this blog post, we outlined the changes coming to the email validation process when requesting and renewing certificates from ACM. We also shared the steps that you can take to prepare for this change, including monitoring at least one of the five relevant email addresses for your domains. Remember that these changes only apply to certificates that use email validation, not certificates that use DNS validation. For more information about certificate management on AWS, see the ACM documentation or get started using ACM today in the AWS Management Console.

If you have questions, contact AWS Support or your technical account manager (TAM), or start a new thread on the AWS re:Post ACM Forum. If you have feedback about this post, submit comments in the Comments section below.

 
Want more AWS Security news? Follow us on Twitter.

Lerna Ekmekcioglu

Lerna Ekmekcioglu

Lerna is a Senior Solutions Architect at AWS where she helps customers build secure, scalable, and highly available workloads. She has over 19 years of platform engineering experience including authentication systems, distributed caching, and multi-Region deployments using IaC and CI/CD to name a few. In her spare time, she enjoys hiking, sightseeing, and backyard astronomy.

Zach Miller

Zach Miller

Zach is a Senior Worldwide Security Specialist Solutions Architect at AWS. His background is in data protection and security architecture, focused on a variety of security domains, including cryptography, secrets management, and data classification. Today, he’s focused on helping enterprise AWS customers adopt and operationalize AWS security services to increase security effectiveness and reduce risk.

Georgy Sebastian

Georgy Sebastian

Georgy is a Senior Software Development Engineer at AWS Cryptography. He has a background in secure system architecture, PKI management, and key distribution. In his free time, he’s an amateur gardener and tinkerer.

Khyati Makim

Khyati Makim

Khyati is a Software Development Manager at AWS Cryptography where she’s focused on building secure solutions with cryptographic best practices. She has 25 years of experience building secure solutions in financial and retail businesses in distributed systems. In her spare time, she enjoys traveling, reading, painting, and spending time with family.

How to implement client certificate revocation list checks at scale with API Gateway

Post Syndicated from Arthur Mnev original https://aws.amazon.com/blogs/security/how-to-implement-client-certificate-revocation-list-checks-at-scale-with-api-gateway/

ityAs you design your Amazon API Gateway applications to rely on mutual certificate authentication (mTLS), you need to consider how your application will verify the revocation status of a client certificate. In your design, you should account for the performance and availability of your verification mechanism to make sure that your application endpoints perform reliably.

In this blog post, I demonstrate an architecture that will help you on your journey to implement custom revocation checks against your certificate revocation list (CRL) for API Gateway. You will also learn advanced Amazon Simple Storage Service (Amazon S3) and AWS Lambda techniques to achieve higher performance and scalability.

Choosing the right certificate verification method

One of your first considerations is whether to use a CRL or the Online Certificate Status Protocol (OCSP), if your certificate authority (CA) offers this option. For an in-depth analysis of these two options, see my earlier blog post, Choosing the right certificate revocation method in ACM Private CA. In that post, I demonstrated that OCSP is a good choice when your application can tolerate high latency or a failure for certificate verification due to TLS service-to-OCSP connectivity. When you rely on mutual TLS authentication in a high-rate transactional environment, increased latency or OCSP reachability failures may affect your application. We strongly recommend that you validate the revocation status of your mutual TLS certificates. Verifying your client certificate status against the CRL is the correct approach for certificate verification if you require reliability and lower, predictable latency. A potential exception to this approach is the use case of AWS Certificate Manager Private Certificate Authority (AWS Private CA) with an OCSP responder hosted on AWS CloudFront.

With an AWS Private CA OCSP responder hosted on CloudFront, you can reduce the risks of network and latency challenges by relying on communication between AWS native services. While this post focuses on the solution that targets CRLs originating from any CA, if you use AWS Private CA with an OCSP responder, you should consider generating an OCSP request in your Lambda authorizer.

Mutual authentication with API Gateway

API Gateway mutual TLS authentication (mTLS) requires you to define a root of trust that will contain your certificate authority public key. During the mutual TLS authentication process, API Gateway performs the undifferentiated heavy lifting by offloading the certificate authentication and negotiation process. During the authentication process, API Gateway validates that your certificate is trusted, has valid dates, and uses a supported algorithm. Additionally, you can refer to the API Gateway documentation and related blog post for details about the mutual TLS authentication process on API Gateway.

Implementing mTLS certificate verification for API Gateway

In the remainder of this blog post, I’ll describe the architecture for a scalable implementation of a client certificate verification mechanism against a CRL on your API Gateway.

The certificate CRL verification process presented here relies on a custom Lambda authorizer that validates the certificate revocation status against the CRL. The Lambda authorizer caches CRL data to optimize the query time for subsequent requests and allows you to define custom business logic that could go beyond CRL verification. For example, you could include other, just-in-time authorization decisions as a part of your evaluation logic.

Implementation mechanisms

This section describes the implementation mechanisms that help you create a high-performing extension to the API Gateway mutual TLS authentication process.

Data repository for your certificate revocation list

API Gateway mutual TLS configuration uses Amazon S3 as a repository for your root of trust. The design for this sample implementation extends the use of S3 buckets to store your CRL and the public key for the certificate authority that signed the CRL.

We strongly recommend that you maintain an updated CRL and verify its signature before data processing. This process is automatic if you use AWS Private CA, because AWS Private CA will update your CRL automatically on revocation. AWS Private CA also allows you to retrieve the CA’s public key by using an API call.

Certificate validation

My sample implementation architecture uses the API Gateway Lambda authorizer to validate the serial number of the client certificate used in the mutual TLS authentication session against the list of serial numbers present in the CRL you publish to the S3 bucket. In the process, the API Gateway custom authorizer will read the client certificate serial number, read and validate the CRL’s digital signature, search for the client’s certificate serial number within the CRL, and return the authorization policy based on the findings.

Optimizing for performance

The mechanisms that enable a predictable, low-latency performance are CRL preprocessing and caching. Your CRL is an ASN.1 data structure that requires a relatively high computing time for processing. Preprocessing your CRL into a simple-to-parse data structure reduces the computational cost you would otherwise incur for every validation; caching the CRL will help you reduce the validation latency and improve predictability further.

Performance optimizations

The process of parsing and validating CRLs is computationally expensive. In the case of large CRL files, parsing the CRL in the Lambda authorizer on every request can result in high latency and timeouts. To improve latency and reduce compute costs, this solution optimizes for performance by preprocessing the CRL and implementing function-level caching.

Preprocessing and generation of a cached CRL file

The first optimization happens when S3 receives a new CRL object. As shown in Figure 1, the S3 PutObject event invokes a preprocessing Lambda that validates the signature of your uploaded CRL and decodes its ASN.1 format. The output of the preprocessing Lambda function is the list of the revoked certificate serial numbers from the CRL, in a data structure that is simpler to read by your programming language of choice, and that won’t require extensive parsing by your Lambda authorizer. The asynchronous approach mitigates the impact of CRL processing on your API Gateway workload.

Figure 1: Sample implementation flow of the pre-processing component

Figure 1: Sample implementation flow of the pre-processing component

Client certificate lookup in a CRL

The optimization happens as part of your Lambda authorizer that retrieves the preprocessed CRL data generated from the first step and searches through the data structure for your client certificate serial number. If the Lambda authorizer finds your client’s certificate serial number in the CRL, the authorization request fails, and the Lambda authorizer generates a “Deny” policy. Searching through a read-optimized data structure prepared by your preprocessing step is the second optimization that reduces the lookup time and the compute requirements.

Function-level caching

Because of the preprocessing, the Lambda authorizer code no longer needs to perform the expensive operation of decoding the ASN.1 data structures of the original CRL; however, network transfer latency will remain and may impact your application.

To improve performance, and as a third optimization, the Lambda service retains the runtime environment for a recently-run function for a non-deterministic period of time. If the function is invoked again during this time period, the Lambda function doesn’t have to initialize and can start running immediately. This is called a warm start. Function-level caching takes advantage of this warm start to hold the CRL data structure in memory persistently between function invocations so the Lambda function doesn’t have to download the preprocessed CRL data structure from S3 on every request.

The duration of the Lambda container’s warm state depends on multiple factors, such as usage patterns and parallel requests processed by your function. If, in your case, API use is infrequent or its usage pattern is spiky, pre-provisioned concurrency is another technique that can further reduce your Lambda startup times and the duration of your warm cache. Although provisioned concurrency does have additional costs, I recommend you evaluate its benefits for your specific environment. You can also check out the blog dedicated to this topic, Scheduling AWS Lambda Provisioned Concurrency for recurring peak usage.

To validate that the Lambda authorizer has the latest copy of the CRL data structure, the S3 ETag value is used to determine if the object has changed. The preprocessed CRL object’s ETag value is stored as a Lambda global variable, so its value is retained between invocations in the same runtime environment. When API Gateway invokes the Lambda authorizer, the function checks for existing global preprocessed CRL data structure and ETag variables. The process will only retrieve a read-optimized CRL when the ETag is absent, or its value differs from the ETag of the preprocessed CRL object in S3.

Figure 2 demonstrates this process flow.

Figure 2: Sample implementation flow for the Lambda authorizer component

Figure 2: Sample implementation flow for the Lambda authorizer component

In summary, you will have a Lambda container with a persistent in-memory lookup data structure for your CRL by doing the following:

  • Asynchronously start your preprocessing workflow by using the S3 PutObject event so you can generate and store your preprocessed CRL data structure in a separate S3 object.
  • Read the preprocessed CRL from S3 and its ETag value and store both values in global variables.
  • Compare the value of the ETag stored in your global variables to the current ETag value of the preprocessed CRL S3 object, to reduce unnecessary downloads if the current ETag value of your S3 object is the same as the previous value.
  • We recommend that you avoid using built-in API Gateway Lambda authorizer result caching, because the status of your certificate might change, and your authorization decision would rest on out-of-date verification results.
  • Consider setting a reserved concurrency for your CRL verification function so that API Gateway can invoke your function even if the overall capacity for your account in your AWS Region is exhausted.

The sample implementation flow diagram in Figure 3 demonstrates the overall architecture of the solution.

Figure 3: Sample implementation flow for the overall CRL verification architecture

Figure 3: Sample implementation flow for the overall CRL verification architecture

The workflow for the solution overall is as follows:

  1. An administrator publishes a CRL and its signing CA’s certificate to their non-public S3 bucket, which is accessible by the Lambda authorizer and preprocessor roles.
  2. An S3 event invokes the Lambda preprocessor to run upon CRL upload. The function retrieves the CRL from S3, validates its signature against the issuing certificate, and parses the CRL.
  3. The preprocessor Lambda stores the results in an S3 bucket with a name in the form <crlname>.cache.json.
  4. A TLS client requests an mTLS connection and supplies its certificate.
  5. API Gateway completes mTLS negotiation and invokes the Lambda authorizer.
  6. The Lambda authorizer function parses the client’s mTLS certificate, retrieves the cached CRL object, and searches the object for the serial number of the client’s certificate.
  7. The authorizer function returns a deny policy if the certificate is revoked or in error.
  8. API Gateway, if authorized, proceeds with the integrated function or denies the client’s request.

Conclusion

In this post, I presented a design for validating your API Gateway mutual TLS client certificates against a CRL, with support for extra-large certificate revocation files. This approach will help you align with the best security practices for validating client certificates and use advanced S3 access and Lambda caching techniques to minimize time and latency for validation.

If you have feedback about this post, submit comments in the Comments section below. If you have questions about this post, start a new thread on the AWS Security, Identity, and Compliance re:Post or contact AWS Support.

Arthur Mnev

Arthur is a Senior Specialist Security Architect for AWS Industries. He spends his day working with customers and designing innovative approaches to help customers move forward with their initiatives, improve their security posture, and reduce security risks in their cloud journeys. Outside of work, Arthur enjoys being a father, skiing, scuba diving, and Krav Maga.

Rafael Cassolato de Meneses

Rafael Cassolato de Meneses

Rafael Cassolato is a Solutions Architect with 20+ years in IT, holding bachelor’s and master’s degrees in Computer Science and 10 AWS certifications. Specializing in migration and modernization, Rafael helps strategic AWS customers achieve their business goals and solve technical challenges by leveraging AWS’s cloud platform.

Decrypting Zabbix TLS with Wireshark

Post Syndicated from Markku Leiniö original https://blog.zabbix.com/decrypting-zabbix-tls-with-wireshark/26832/

One of the built-in security features in Zabbix is TLS (Transport Layer Security) support for external connections. This means that when your distributed Zabbix proxies or Zabbix agents connect to the Zabbix server (or vice versa), TLS can be used to encrypt all the connections. When the connections are encrypted, third parties cannot read the Zabbix components’ communication, even though they would be able to catch the network traffic in some way.

In specific cases you may still want to inspect the encrypted traffic, for example to troubleshoot some problems with Zabbix agents or proxies. I already wrote a post about troubleshooting Zabbix agent with Wireshark, but the TLS encryption prevents anyone seeing the actual contents of the packets.

Since the traffic is encrypted in the Zabbix components (the server, agents and proxies), there still is a way for you, the Zabbix administrator, to intervene with the encryption so that you can get hold of the unencrypted traffic as well. In this post I will explain the process.

First, let’s demonstrate the TLS encryption between a Zabbix agent and a Zabbix server. I have configured the agent (Zabbix Agent 2 actually) with these lines:

Hostname=Zabbix70-agent
ServerActive=zabbixtest.lein.io
TLSConnect=psk
TLSPSKIdentity=agent-ident
TLSPSKFile=/etc/zabbix/psk

In this example I’m using TLS with pre-shared key (PSK), and the key itself is saved in /etc/zabbix/psk. My favorite way of generating a PSK is using OpenSSL:

markku@agent:~$ openssl rand -hex 32
afa34bf1104a1457e11e7d3a9b1ff7f5fb4f494c92ca1a8a9c5e1437f8897416
markku@agent:~$

The same key must also be configured on the Zabbix server frontend, see the Zabbix documentation for the PSK configuration details:

After the configurations I captured the Zabbix traffic for some time on the Zabbix server (using sudo tcpdump port 10051 -v -w zabbix70-tls-agent.pcap), stopped the capture, copied the capture file to my workstation, and opened it with Wireshark.

The capture file can be downloaded here:

Note: I recommend using Wireshark version 4.1.0 or later when analyzing captures containing Zabbix traffic because the built-in Zabbix protocol support was only added to Wireshark in version 4.1.0.

The packet list looks like this:

As we can see in the Protocol column, there are no Zabbix packets recognized in this capture, there are only TCP and TLS packets (the TCP-marked packets being the “empty” packets for negotiating the actual connectivity).

A side detail: Even though the traffic is encrypted, you can still see the configured Zabbix TLS PSK identity (“agent-ident” in my configuration above) in plain text inside the TLS Client Hello packets, if you ever need to check that in the traffic.

Now that we confirmed that TLS encryption is used and we cannot see the Zabbix traffic contents in the capture, let’s prepare the Zabbix server for the TLS decryption.

As I hinted in the beginning, since we have the TLS connection endpoints under our management, we can do tricks on the hosts to get the encryption keys. TLS negotiates the encryption keys dynamically for each connection, but there is a way to save the keys to a file so that we can later decrypt the captured traffic. (Note: I’m not a protocol-level TLS expert, so please forgive me any possible technical inaccuracies in the detailed explanations. I’ll just call “TLS keys” whatever is needed to get the encryption/decryption done.)

Peter Wu (who, in contrast to me, is a protocol-level TLS expert, and also one of the Wireshark core developers) has kindly published code for a helper library that makes it possible for us to save the TLS session keys on the TLS endpoint. In this demo I will save the keys on the Zabbix server, but the same could be done on the agents/proxies instead if needed.

First I’ll see the TLS library that my Debian-based Zabbix server is using:

markku@zabbixserver:~$ ldd /usr/sbin/zabbix_server | grep ssl
        libssl.so.3 => /lib/x86_64-linux-gnu/libssl.so.3 (0x00007f62ee47a000)
markku@zabbixserver:~$ dpkg -l libssl* | grep ^ii
ii  libssl3:amd64  3.0.9-1   amd64  Secure Sockets Layer toolkit - shared libraries
markku@zabbixserver:~$

To get and compile the helper library I’ll need to install some utilities:

markku@zabbixserver:~$ sudo apt install git gcc make libssl-dev
...
markku@zabbixserver:~$ dpkg -l libssl* | grep ^ii
ii  libssl-dev:amd64 3.0.9-1 amd64 Secure Sockets Layer toolkit - development files
ii  libssl3:amd64    3.0.9-1 amd64 Secure Sockets Layer toolkit - shared libraries
markku@zabbixserver:~$

I’ll the clone the Peter’s wireshark-notes repo to the server:

markku@zabbixserver:~$ git clone --depth=1 https://git.lekensteyn.nl/peter/wireshark-notes
Cloning into 'wireshark-notes'...
...
markku@zabbixserver:~$ cd wireshark-notes/src
markku@zabbixserver:~/wireshark-notes/src$ ls -l
total 28
-rw-r--r-- 1 markku markku   534 Oct  7 15:39 Makefile
-rw-r--r-- 1 markku markku 11392 Oct  7 15:39 sslkeylog.c
-rw-r--r-- 1 markku markku  7278 Oct  7 15:39 sslkeylog.py
-rwxr-xr-x 1 markku markku  2325 Oct  7 15:39 sslkeylog.sh
markku@zabbixserver:~/wireshark-notes/src$

Now I can compile the library and make it available on the server:

markku@zabbixserver:~/wireshark-notes/src$ make
cc   sslkeylog.c -shared -o libsslkeylog.so -fPIC -ldl
markku@zabbixserver:~/wireshark-notes/src$ sudo install libsslkeylog.so /usr/local/lib
markku@zabbixserver:~/wireshark-notes/src$ ls -l /usr/local/lib/libsslkeylog.so
-rwxr-xr-x 1 root root 17336 Oct  7 15:40 /usr/local/lib/libsslkeylog.so
markku@zabbixserver:~/wireshark-notes/src$ cd
markku@zabbixserver:~$

To use the helper library, a couple of environment variables need to be set. For Zabbix server the easy way is to edit the systemd configuration for zabbix-server service:

markku@zabbixserver:~$ sudo systemctl edit zabbix-server

In the editor that opens I’ll add these in the configuration:

[Service]
Environment=LD_PRELOAD=/usr/local/lib/libsslkeylog.so
Environment=SSLKEYLOGFILE=/tmp/tls.keys

The variables are kind of self-explanatory: Whenever Zabbix server service is started, the libsslkeylog.so library is loaded first, and the SSLKEYLOGFILE variable sets the location of the file where the keys will be saved.

Now the word of warning: The libsslkeylog.so library, when loaded by a process that uses TLS communication, will save the encryption/decryption keys of all the TLS sessions of the process to the configured file. This means that whoever gets that file and the saved TLS communication will be able to see the decrypted contents of the packets, defeating the whole idea of the TLS encryption. You really don’t want to do this TLS key saving for any longer periods of time. Be sure to remove the configurations (and restart the service) after you have inspected whatever you were inspecting in your system. Or, don’t do any of this at all.

After saving the configuration the Zabbix server needs to be restarted:

markku@zabbixserver:~$ sudo systemctl restart zabbix-server
markku@zabbixserver:~$

The TLS keys have now started being saved in the configured file:

markku@zabbixserver:~$ ls -l /tmp/tls.keys
-rw-rw-r-- 1 zabbix zabbix 10157 Oct  7 15:45 tls.keys
markku@zabbixserver:~$

At this point the Zabbix agent is still communicating actively with the Zabbix server, so I’ll take a new capture with tcpdump (sudo tcpdump port 10051 -v -w zabbix70-tls-agent-2.pcap).

After a short while I’ll stop the capture, and copy the capture file and the TLS key file on my workstation.

Now it’s a good time to disable the TLS key saving as well (besides containing sensitive data, the key file will also grow with each new TLS session so it can quickly get very large), so I’ll edit the Zabbix service configuration, remove the configured lines and restart the service:

markku@zabbixserver:~$ sudo systemctl edit zabbix-server
markku@zabbixserver:~$ sudo systemctl restart zabbix-server
markku@zabbixserver:~$

When opening the new capture file in Wireshark there is no immediate change in the packet list: the TLS packets are still shown encrypted. Wireshark needs to be specifically configured to read the TLS keys from the separate file.

In Wireshark, I’ll go to Edit – Preferences – Protocols – TLS:

There is the “(Pre)-Master-Secret log filename” field, I’ll use Browse button to select the copied tls.keys file, and save the configuration with OK.

At this point Wireshark reloads the capture file and the Zabbix agent TLS sessions will be decrypted:

Using the “zabbix” display filter will show just the Zabbix protocol packets:

When selecting a Zabbix protocol packet and looking at the packet details, in the lower right pane there are now three tabs: Frame (the encrypted TLS data), Decrypted TLS, and Uncompressed data.

This is because in this example the Zabbix agent 2 also compresses the traffic, and the compressed traffic is then encrypted when sending out to the network. Wireshark can interpret all this because of its built-in knowledge about TLS encryption and the Zabbix protocol structure, as well as the user-supplied TLS decryption keys.

We are now able to analyze the Zabbix agent communication with Wireshark even though the traffic was TLS-encrypted when we captured it.

One more trick about the TLS keys in Wireshark: It is also possible to save the keys inside the capture file when analyzing the traffic, instead of having the keys in a separate file (tls.keys in this example). I’ll go in Edit menu and select Inject TLS Secrets, and then save the capture file in pcapng format. Now the previously loaded keys are embedded in the capture file, and I can clear the “(Pre)-Master-Secret log filename” field in the TLS settings (as the filename setting is not useful in any later Wireshark analysis). The same can also be done in the command line by using editcap --inject-secrets (editcap is part of Wireshark install, see the manual page of editcap for more details).

Here is the second capture file of this demo, with the embedded TLS keys:

Finally some closing comments:

  • As demonstrated, when you have administrator/root-level access to the TLS session endpoint (Zabbix server in this example), there can be a possibility to save and decrypt the TLS sessions using external tooling. After all, TLS encryption is based on the negotiation between the TLS-connected endpoints, so if you are the TLS connection endpoint, you have ways to access the plaintext data. If you don’t have sufficient access to the TLS session endpoint, there is no way you can get the decryption keys mid-path.
  • Act responsibly when saving the TLS session keys for any traffic, on Zabbix server or otherwise. The encryption is there for a purpose, and saving the TLS keys always carries the risk that someone else gets access to data they wouldn’t have access to otherwise.
  • Do not save the TLS session keys with the capture file, unless you are dealing with a test/demo environment, like I had here.
  • When troubleshooting Zabbix connections, TLS decryption with Wireshark is not the only way. You should also consider if just increasing the logging level in the Zabbix components brings you enough information to solve your case, or maybe in some specific case you can just disable TLS encryption for an agent for a moment to not have to deal with the decryption at all. But again, usually the encryption is there for a purpose, so you need to evaluate your own situation.

The post Decrypting Zabbix TLS with Wireshark appeared first on Zabbix Blog.

Messaging Service Wiretap Discovered through Expired TLS Cert

Post Syndicated from Bruce Schneier original https://www.schneier.com/blog/archives/2023/10/messaging-service-wiretap-discovered-through-expired-tls-cert.html

Fascinating story of a covert wiretap that was discovered because of an expired TLS certificate:

The suspected man-in-the-middle attack was identified when the administrator of jabber.ru, the largest Russian XMPP service, received a notification that one of the servers’ certificates had expired.

However, jabber.ru found no expired certificates on the server, ­ as explained in a blog post by ValdikSS, a pseudonymous anti-censorship researcher based in Russia who collaborated on the investigation.

The expired certificate was instead discovered on a single port being used by the service to establish an encrypted Transport Layer Security (TLS) connection with users. Before it had expired, it would have allowed someone to decrypt the traffic being exchanged over the service.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Post Syndicated from Suleman Ahmad original http://blog.cloudflare.com/connection-coalescing-with-origin-frames-fewer-dns-queries-fewer-connections/

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

This blog reports and summarizes the contents of a Cloudflare research paper which appeared at the ACM Internet Measurement Conference, that measures and prototypes connection coalescing with ORIGIN Frames.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Some readers might be surprised to hear that a single visit to a web page can cause a browser to make tens, sometimes even hundreds, of web connections. Take this very blog as an example. If it is your first visit to the Cloudflare blog, or it has been a while since your last visit, your browser will make multiple connections to render the page. The browser will make DNS queries to find IP addresses corresponding to blog.cloudflare.com and then subsequent requests to retrieve any necessary subresources on the web page needed to successfully render the complete page. How many? Looking below, at the time of writing, there are 32 different hostnames used to load the Cloudflare Blog. That means 32 DNS queries and at least 32 TCP (or QUIC) connections, unless the client is able to reuse (or coalesce) some of those connections.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Each new web connection not only introduces additional load on a server's processing capabilities – potentially leading to scalability challenges during peak usage hours – but also exposes client metadata to the network, such as the plaintext hostnames being accessed by an individual. Such meta information can potentially reveal a user’s online activities and browsing behaviors to on-path network adversaries and eavesdroppers!

In this blog we’re going to take a closer look at “connection coalescing”. Since our initial look at IP-based coalescing in 2021, we have done further large-scale measurements and modeling across the Internet, to understand and predict if and where coalescing would work best. Since IP coalescing is difficult to manage at large scale, last year we implemented and experimented with a promising standard called the HTTP/2 ORIGIN Frame extension that we leveraged to coalesce connections to our edge without worrying about managing IP addresses.

All told, there are opportunities being missed by many large providers. We hope that this blog (and our publication at ACM IMC 2022 with full details) offers a first step that helps servers and clients take advantage of the ORIGIN Frame standard.

Setting the stage

At a high level, as a user navigates the web, the browser renders web pages by retrieving dependent subresources to construct the complete web page. This process bears a striking resemblance to the way physical products are assembled in a factory. In this sense, a modern web page can be considered like an assembly plant. It relies on a ‘supply chain’ of resources that are needed to produce the final product.

An assembly plant in the physical world can place a single order for different parts and get a single shipment from the supplier (similar to the kitting process for maximizing value and minimizing response time); no matter the manufacturer of those parts or where they are made — one ‘connection’ to the supplier is all that is needed. Any single truck from a supplier to an assembly plant can be filled with parts from multiple manufacturers.

The design of the web causes browsers to typically do the opposite in nature. To retrieve the images, JavaScript, and other resources on a web page (the parts), web clients (assembly plants) have to make at least one connection to every hostname (the manufacturers) defined in the HTML that is returned by the server (the supplier). It makes no difference if the connections to those hostnames go to the same server or not, for example they could go to a reverse proxy like Cloudflare. For each manufacturer a ‘new’ truck would be needed to transfer the materials to the assembly plant from the same supplier, or more formally, a new connection would need to be made to request a subresource from a hostname on the same web page.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections
Without connection coalescing

The number of connections used to load a web page can be surprisingly high. It is also common for the subresources to need yet other sub-subresources, and so new connections emerge as a result of earlier ones. Remember, too, that HTTP connections to hostnames are often preceded by DNS queries! Connection coalescing allows us to use fewer connections, or ‘reuse’ the same set of trucks to carry parts from multiple manufacturers from a single supplier.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections
With connection coalescing 

Connection coalescing in principle

Connection coalescing was introduced in HTTP/2, and carried over into HTTP/3. We’ve blogged about connection coalescing previously (for a detailed primer we encourage going over that blog). While the idea is simple, implementing it can present a number of engineering challenges. For example, recall from above that there are 32 hostnames (at the time of writing) to load the web page you are reading right now. Among the 32 hostnames are 16 unique domains (defined as “Effective TLD+1”). Can we create fewer connections or ‘coalesce’ existing connections for each unique domain? The answer is ‘Yes, but it depends’.

The exact number of connections to load the blog page is not at all obvious, and hard to know. There may be 32 hostnames attached to 16 domains but, counter-intuitively, this does not mean the answer to “how many unique connections?” is 16. The true answer could be as few as one connection if all the hostnames are reachable at a single server; or as many as 32 independent connections if a different and distinct server is needed to access each individual hostname.

Connection reuse comes in many forms, so it’s important to define “connection coalescing” in the HTTP space. For example, the reuse of an existing TCP or TLS connection to a hostname to make multiple requests for subresources from that same hostname is connection reuse, but not coalescing.

Coalescing occurs when an existing TLS channel for some hostname can be repurposed or used for connecting to a different hostname. For example, upon visiting blog.cloudflare.com, the HTML points to subresources at cdnjs.cloudflare.com. To reuse the same TLS connection for the subresources, it is necessary for both hostnames to appear together in the TLS certificate's “Server Alternative Name (SAN)” list, but this step alone is not sufficient to convince browsers to coalesce. After all, the cdnjs.cloudflare.com service may or may not be reachable at the same server as blog.cloudflare.com, despite being on the same certificate. So how can the browser know? Coalescing only works if servers set up the right conditions, but clients have to decide whether to coalesce or not – thus, browsers require a signal to coalesce beyond the SANs list on the certificate. Revisiting our analogy, the assembly plant may order a part from a manufacturer directly, not knowing that the supplier already has the same part in its warehouse.

There are two explicit signals a browser can use to decide whether connections can be coalesced: one is IP-based, the other ORIGIN Frame-based. The former requires the server operators to tightly bind DNS records to the HTTP resources available on the server. This is difficult to manage and deploy, and actually creates a risky dependency, because you have to place all the resources behind a specific set or a single IP address. The way IP addresses influence coalescing decisions varies among browsers, with some choosing to be more conservative and others more permissive. Alternatively, the HTTP ORIGIN Frame is an easier signal for the servers to orchestrate; it’s also flexible and has graceful failure with no interruption to service (for a specification compliant implementation).

A foundational difference between both these coalescing signals is: IP-based coalescing signals are implicit, even accidental, and force clients to infer coalescing possibilities that may exist, or not. None of this is surprising since IP addresses are designed to have no real relationship with names! In contrast, ORIGIN Frame is an explicit signal from servers to clients that coalescing is available no matter what DNS says for any particular hostname.

We have experimented with IP-based coalescing previously; for the purpose of this blog we will take a deeper look at ORIGIN Frame-based coalescing.

What is the ORIGIN Frame standard?

The ORIGIN Frame is an extension to the HTTP/2 and HTTP/3 specification, a special Frame sent on stream 0 or the control stream of the connection respectively. The Frame allows the servers to send an ‘origin-set’ to the clients on an existing established TLS connection, which includes hostnames that it is authorized for and will not incur any HTTP 421 errors. Hostnames in the origin-set MUST also appear in the certificate SAN list for the server, even if those hostnames are announced on different IP addresses via DNS.

Specifically, two different steps are required:

  1. Web servers must send a list enumerating the Origin Set (the hostnames that a given connection might be used for) in the ORIGIN Frame extension.
  2. The TLS certificate returned by the web server must cover the additional hostnames being returned in the ORIGIN Frame in the DNS names SAN entries.

At a high-level ORIGIN Frames are a supplement to the TLS certificate that operators can attach to say, “Psst! Hey, client, here are the names in the SANs that are available on this connection — you can coalesce!” Since the ORIGIN Frame is not part of the certificate itself, its contents can be made to change independently. No new certificate is required. There is also no dependency on IP addresses. For a coalesceable hostname, existing TCP/QUIC+TLS connections can be reused without requiring new connections or DNS queries.

Many websites today rely on content which is served by CDNs, like Cloudflare CDN service. The practice of using external CDN services offers websites the advantages of speed, reliability, and reduces the load of content served by their origin servers. When both the website, and the resources are served by the same CDN, despite being different hostnames, owned by different entities, it opens up some very interesting opportunities for CDN operators to allow connections to be reused and coalesced since they can control both the certificate management and connection requests for sending ORIGIN frames on behalf of the real origin server.

Unfortunately, there has been no way to turn the possibilities enabled by ORIGIN Frame into practice. To the best of our knowledge, until today, there has been no server implementation that supports ORIGIN Frames. Among browsers, only Firefox supports ORIGIN Frames. Since IP coalescing is challenging and ORIGIN Frame has no deployed support, is the engineering time and energy to better support coalescing worth the investment? We decided to find out with a large-scale Internet-wide measurement to understand the opportunities and predict the possibilities, and then implemented the ORIGIN Frame to experiment on production traffic.

Experiment #1: What is the scale of required changes?

In February 2021, we collected data for 500K of the most popular websites on the Internet, using a modified Web Page Test on 100 virtual machines. An automated Chrome (v88) browser instance was launched for every visit to a web page to eliminate caching effects (because we wanted to understand coalescing, not caching). On successful completion of each session, Chrome developer tools were used to retrieve and write the page load data as an HTTP Archive format (HAR) file with a full timeline of events, as well as additional information about certificates and their validation. Additionally, we parsed the certificate chains for the root web page and new TLS connections triggered by subresource requests to (i) identify certificate issuers for the hostnames, (ii) inspect the presence of the Subject Alternative Name (SAN) extension, and (iii) validate that DNS names resolve to the IP address used. Further details about our methodology and results can be found in the technical paper.

The first step was to understand what resources are requested by web pages to successfully render the page contents, and where these resources were present on the Internet. Connection coalescing becomes possible when subresource domains are ideally co-located. We approximated the location of a domain by finding its corresponding autonomous system (AS). For example, the domain attached to cdnjs is reachable via AS 13335 in the BGP routing table, and that AS number belongs to Cloudflare. The figure below describes the percentage of web pages and the number of unique ASes needed to fully load a web page.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Around 14% of the web pages need two ASes to fully load i.e. pages that have a dependency on one additional AS for subresources. More than 50% of the web pages need to contact no more than six ASes to obtain all the necessary subresources. This finding as shown in the plot above implies that a relatively small number of operators serve the sub-resource content necessary for a majority (~50%) of the websites, and any usage of ORIGIN Frames would need only a few changes to have its intended impact. The potential for connection coalescing can therefore be optimistically approximated to the number of unique ASes needed to retrieve all subresources in a web page. In practice however, this may be superseded by operational factors such as SLAs or helped by flexible mappings between sockets, names, and IP addresses which we worked on previously at Cloudflare.

We then tried to understand the impact of coalescing on connection metrics. The measured and ideal number of DNS queries and TLS connections needed to load a web page are summarized by their CDFs in the figure below.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Through modeling and extensive analysis, we identify that connection coalescing through ORIGIN Frames could reduce the number of DNS and TLS connections made by browsers by over 60% at the median. We performed this modeling by identifying the number of times the clients requested DNS records, and combined them with the ideal ORIGIN Frames to serve.

Many multi-origin servers such as those operated by CDNs tend to reuse certificates and serve the same certificate with multiple DNS SAN entries. This allows the operators to manage fewer certificates through their creation and renewal cycles. While theoretically one can have millions of names in the certificate, creating such certificates is unreasonable and a challenge to manage effectively. By continuing to rely on existing certificates, our modeling measurements bring to light the volume of changes required to enable perfect coalescing, while presenting information about the scale of changes needed, as highlighted in the figure below.

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

We identify that over 60% of the certificates served by websites do not need any modifications and could benefit from ORIGIN Frames, while with no more than 10 additions to the DNS SAN names in certificates we’re able to successfully coalesce connections to over 92% of the websites in our measurement. The most effective changes could be made by CDN providers by adding three or four of their most popular requested hostnames into each certificate.

Experiment #2: ORIGIN Frames in action

In order to validate our modeling expectations, we then took a more active approach in early 2022. Our next experiment focused on 5,000 websites that make extensive use of cdnjs.cloudflare.com as a subresource. By modifying our experimental TLS termination endpoint we deployed HTTP/2 ORIGIN Frame support as defined in the RFC standard. This involved changing the internal fork of net and http dependency modules of Golang which we have open sourced (see here, and here).

During the experiments, connecting to a website in the experiment set would return cdnjs.cloudflare.com in the ORIGIN frame, while the control set returned an arbitrary (unused) hostname. All existing edge certificates for the 5000 websites were also modified. For the experimental group, the corresponding certificates were renewed with cdnjs.cloudflare.com added to the SAN. To ensure integrity between control and experimental sets, control group domains certificates were also renewed with a valid and identical size third party domain used by none of the control domains. This is done to ensure that the relative size changes to the certificates is kept constant avoiding potential biases due to different certificate sizes. Our results were striking!

Connection coalescing with ORIGIN Frames: fewer DNS queries, fewer connections

Sampling 1% of the requests we received from Firefox to the websites in the experiment, we identified over 50% reduction in new TLS connections per second indicating a lesser number of cryptographic verification operations done by both the client and reduced server compute overheads. As expected there were no differences in the control set indicating the effectiveness of connection re-use as seen by the CDN or server operators.

Discussion and insights

While our modeling measurements indicated that we could anticipate some performance improvements, in practice it was not significantly better suggesting that ‘no-worse’ is the appropriate mental model regarding performance. The subtle interplay between resource object sizes, competing connections, and congestion control is subject to network conditions. Bottleneck-share capacity, for example, diminishes as fewer connections compete for bottleneck resources on network links. It would be interesting to revisit these measurements as more operators deploy support on their servers for ORIGIN Frames.

Apart from performance, one major benefit of ORIGIN frames is in terms of privacy. How? Well, each coalesced connection hides client metadata that is otherwise leaked from non-coalesced connections. Certain resources on a web page are loaded depending on how one is interacting with the website. This means for every new connection for retrieving some resource from the server, TLS plaintext metadata like SNI (in the absence of Encrypted Client Hello) and at least one plaintext DNS query, if transmitted over UDP or TCP on port 53, is exposed to the network. Coalescing connections helps remove the need for browsers to open new TLS connections, and the need to do extra DNS queries. This prevents metadata leakage from anyone listening on the network. ORIGIN Frames help minimize those signals from the network path, improving privacy by reducing the amount of cleartext information leaked on path to network eavesdroppers.

While the browsers benefit from reduced cryptographic computations needed to verify multiple certificates, a major advantage comes from the fact that it opens up very interesting future opportunities for resource scheduling at the endpoints (the browsers, and the origin servers) such as prioritization, or recent proposals like HTTP early hints to provide clients experiences where connections are not overloaded or competing for those resources. When coupled with CERTIFICATE Frames IETF draft, we can further eliminate the need for manual certificate modifications as a server can prove its authority of hostnames after connection establishment without any additional SAN entries on the website’s TLS certificate.

Conclusion and call to action

In summary, the current Internet ecosystem has a lot of opportunities for connection coalescing with only a few changes to certificates and their server infrastructure. Servers can significantly reduce the number of TLS handshakes by roughly 50%, while reducing the number of render blocking DNS queries by over 60%. Clients additionally reap these benefits in privacy by reducing cleartext DNS exposure to network on-lookers.

To help make this a reality we are currently planning to add support for both HTTP/2 and HTTP/3 ORIGIN Frames for our customers. We also encourage other operators that manage third party resources to adopt support of ORIGIN Frame to improve the Internet ecosystem.
Our paper submission was accepted to the ACM Internet Measurement Conference 2022 and is available for download. If you’d like to work on projects like this, where you get to see the rubber meet the road for new standards, visit our careers page!

Introducing per hostname TLS settings — security fit to your needs

Post Syndicated from Dina Kozlov original http://blog.cloudflare.com/introducing-per-hostname-tls-settings/

Introducing per hostname TLS settings — security fit to your needs

Introducing per hostname TLS settings — security fit to your needs

One of the goals of Cloudflare is to give our customers the necessary knobs to enable security in a way that fits their needs. In the realm of SSL/TLS, we offer two key controls: setting the minimum TLS version, and restricting the list of supported cipher suites. Previously, these settings applied to the entire domain, resulting in an “all or nothing” effect. While having uniform settings across the entire domain is ideal for some users, it sometimes lacks the necessary granularity for those with diverse requirements across their subdomains.

It is for that reason that we’re excited to announce that as of today, customers will be able to set their TLS settings on a per-hostname basis.

The trade-off with using modern protocols

In an ideal world, every domain could be updated to use the most secure and modern protocols without any setbacks. Unfortunately, that's not the case. New standards and protocols require adoption in order to be effective. TLS 1.3 was standardized by the IETF in April 2018. It removed the vulnerable cryptographic algorithms that TLS 1.2 supported and provided a performance boost by requiring only one roundtrip, as opposed to two. For a user to benefit from TLS 1.3, they need their browser or device to support the new TLS version. For modern browsers and devices, this isn’t a problem – these operating systems are built to dynamically update to support new protocols. But legacy clients and devices were, obviously, not built with the same mindset. Before 2015, new protocols and standards were developed over decades, not months or years, so the clients were shipped out with support for one standard — the one that was used at the time.

If we look at Cloudflare Radar, we can see that about 62.9% of traffic uses TLS 1.3. That’s quite significant for a protocol that was only standardized 5 years ago. But that also means that a significant portion of the Internet continues to use TLS 1.2 or lower.

The same trade-off applies for encryption algorithms. ECDSA was standardized in 2005, about 20 years after RSA. It offers a higher level of security than RSA and uses shorter key lengths, which adds a performance boost for every request. To use ECDSA, a domain owner needs to obtain and serve an ECDSA certificate and the connecting client needs to support cipher suites that use elliptical curve cryptography (ECC). While most publicly trusted certificate authorities now support ECDSA-based certificates, the slow rate of adoption has led many legacy systems to only support RSA, which means that restricting applications to only support ECC-based algorithms could prevent access from those that use older clients and devices.

Balancing the trade-offs

When it comes to security and accessibility, it’s important to find the right middle ground for your business.

To maintain brand, most companies deploy all of their assets under one domain. It’s common for the root domain (e.g. example.com) to be used as a marketing website to provide information about the company, its mission, and the products and services it offers. Then, under the same domain, you might have your company blog (e.g. blog.example.com), your management portal (e.g. dash.example.com), and your API gateway (e.g. api.example.com).

The marketing website and the blog are similar in that they’re static sites that don’t collect information from the accessing users. On the other hand, the management portal and API gateway collect and present sensitive data that needs to be protected.

When you’re thinking about which settings to deploy, you want to consider the data that’s exchanged and the user base. The marketing website and blog should be accessible to all users. You can set them up to support modern protocols for the clients that support them, but you don’t necessarily want to restrict access for users that are accessing these pages from old devices.

The management portal and API gateway should be set up in a manner that provides the best protection for the data exchanged. That means dropping support for less secure standards with known vulnerabilities and requiring new, secure protocols to be used.

To be able to achieve this setup, you need to be able to configure settings for every subdomain within your domain individually.

Per hostname TLS settings – now available!

Customers that use Cloudflare’s Advanced Certificate Manager can configure TLS settings on individual hostnames within a domain. Customers can use this to enable HTTP/2, or to configure the minimum TLS version and the supported ciphers suites on a particular hostname. Any settings that are applied on a specific hostname will supersede the zone level setting. The new capability also allows you to have different settings on a hostname and its wildcard record; which means you can configure example.com to use one setting, and *.example.com to use another.

Let’s say that you want the default min TLS version for your domain to be TLS 1.2, but for your dashboard and API subdomains, you want to set the minimum TLS version to be TLS 1.3. In the Cloudflare dashboard, you can set the zone level minimum TLS version to 1.2 as shown below. Then, to make the minimum TLS version for the dashboard and API subdomains TLS 1.3, make a call to the per-hostname TLS settings API endpoint with the specific hostname and setting.

Introducing per hostname TLS settings — security fit to your needs

This is all available, starting today, through the API endpoint! And if you’d like to learn more about how to use our per-hostname TLS settings, please jump on over to our developer documentation.

Bring your own CA for client certificate validation with API Shield

Post Syndicated from Dina Kozlov original http://blog.cloudflare.com/bring-your-own-ca-for-client-certificate-validation-with-api-shield/

Bring your own CA for client certificate validation with API Shield

Bring your own CA for client certificate validation with API Shield

APIs account for more than half of the total traffic of the Internet. They are the building blocks of many modern web applications. As API usage grows, so does the number of API attacks. And so now, more than ever, it’s important to keep these API endpoints secure. Cloudflare’s API Shield solution offers a comprehensive suite of products to safeguard your API endpoints and now we’re excited to give our customers one more tool to keep their endpoints safe. We’re excited to announce that customers can now bring their own Certificate Authority (CA) to use for mutual TLS client authentication. This gives customers more security, while allowing them to maintain control around their Mutual TLS configuration.

The power of Mutual TLS (mTLS)

Traditionally, when we refer to TLS certificates, we talk about the publicly trusted certificates that are presented by servers to prove their identity to the connecting client. With Mutual TLS, both the client and the server present a certificate to establish a two-way channel of trust. Doing this allows the server to check who the connecting client is and whether or not they’re allowed to make a request. The certificate presented by the client – the client certificate – doesn’t need to come from a publicly trusted CA. In fact, it usually comes from a private or self-signed CA. That’s because the only party that needs to be able to trust it is the connecting server. As long as the connecting server has the client certificate and can check its validity, it doesn’t need to be public.

Securing API endpoints with Mutual TLS

Mutual TLS plays a crucial role in protecting API endpoints. When it comes to safeguarding these endpoints, it's important to have a security model in place that only allows authorized clients to make requests and keeps everyone else out.

That’s why when we launched API Shield in 2020 – a product that’s centered around securing API endpoints – we included mutual TLS client certificate validation as a part of the offering. We knew that mTLS was the best way for our customers to identify and authorize their connecting clients.

When we launched mutual TLS for API Shield, we gave each of our customers a dedicated self-signed CA that they could use to issue client certificates. Once the certificates are installed on devices and mTLS is set up, administrators can enforce that connections can only be made if they present a client certificate issued from that self-signed CA.

This feature has been paramount in securing thousands of endpoints, but it does require our customer to install new client certificates on their devices, which isn’t always possible. Some customers have been using mutual TLS for years with their own CA, which means that the client certificates are already in the wild. Unless the application owner has direct control over the clients, it’s usually arduous, if not impossible, to replace the client certificates with ones issued from Cloudflare’s CA. Other customers may be required to use a CA issued from an approved third party in order to meet regulatory requirements.

To help all of our customers keep their endpoints secure, we’re extending API Shield’s mTLS capability to allow customers to bring their own CA.

Bring your own CA for client certificate validation with API Shield

Get started today

To simplify the management of private PKI at Cloudflare, we created one account level endpoint that enables customers to upload self-signed CAs to use across different Cloudflare products. Today, this endpoint can be used for API shield CAs and for Gateway CAs that are used for traffic inspection.

If you’re an Enterprise customer, you can upload up to five CAs to your account. Once you’ve uploaded the CA, you can use the API Shield hostname association API to associate the CA with the mTLS enabled hostnames. That will tell Cloudflare to start validating the client certificate against the uploaded CA for requests that come in on that hostname. Before you enforce the client certificate validation, you can create a Firewall rule that logs an event when a valid or invalid certificate is served. That will help you determine if you’ve set things up correctly before you enforce the client certificate validation and drop unauthorized requests.

To learn more about how you can use this, refer to our developer documentation.

If you’re interested in using mutual TLS to secure your corporate network, talk to an account representative about using our Access product to do so.

Faster AWS cloud connections with TLS 1.3

Post Syndicated from Kate Rodgers original https://aws.amazon.com/blogs/security/faster-aws-cloud-connections-with-tls-1-3/

At Amazon Web Services (AWS), we strive to continuously improve customer experience by delivering a cloud computing environment that supports the most modern security technologies. To improve the overall performance of your connections, we have already started to enable TLS version 1.3 globally across our AWS service API endpoints, and will complete this process by December 31, 2023. By using TLS 1.3, you can decrease your connection time by removing one network round trip for every connection request, and can benefit from some of the most modern and secure cryptographic cipher suites available today.

If you are using current software tools (2014 or later) including our AWS SDKs or AWS Command Line Interface (AWS CLI), you will automatically receive the benefits of TLS 1.3 with no action required on your part. This is because AWS services will negotiate the highest TLS protocol version that your client software supports. If you want to continue using TLS 1.2, you will still have full control through your client configurations. AWS will retain support for TLS 1.2, in addition to TLS 1.3, into the foreseeable future. Meanwhile, here’s the latest information on the on-going deprecation of TLS 1.0/1.1.

If you have any questions, start a new thread on AWS re:Post, or contact AWS Support or your technical account manager. If you have feedback about this post, submit comments in the Comments section below.

Want more AWS Security how-to content, news, and feature announcements? Follow us on Twitter.

Kate Rodgers

Kate Rodgers

Kate is a Senior Technical Program Manager in AWS Security with over 10 years of experience in industry as an engineer and program manager. Today she works with AWS services, infrastructure, and administrative teams to drive innovative solutions that improve the AWS security posture.

James McDuffie

James McDuffie

James is a Senior Technical Account Manager. He has over 20 years of experience in software development, with previous roles in Software and Hardware Security Architecture in Industrial IoT. He is an active member of the AWS Security community, and he works closely with our customers to help them solve complex security challenges at scale.

mTLS client certificate revocation vulnerability with TLS Session Resumption

Post Syndicated from Rushil Mehra original https://blog.cloudflare.com/mtls-client-certificate-revocation-vulnerability-with-tls-session-resumption/

mTLS client certificate revocation vulnerability with TLS Session Resumption

mTLS client certificate revocation vulnerability with TLS Session Resumption

On December 16, 2022, Cloudflare discovered a bug where, in limited circumstances, some users with revoked certificates may not have been blocked by Cloudflare firewall settings. Specifically, Cloudflare’s Firewall Rules solution did not block some users with revoked certificates from resuming a session via mutual transport layer security (mTLS), even if the customer had configured Firewall Rules to do so. This bug has been mitigated, and we have no evidence of this being exploited. We notified any customers that may have been impacted in an abundance of caution, so they can check their own logs to determine if an mTLS protected resource was accessed by entities holding a revoked certificate.

What happened?

One of Cloudflare Firewall Rules’ features, introduced in March 2021, lets customers revoke or block a client certificate, preventing it from being used to authenticate and establish a session. For example, a customer may use Firewall Rules to protect a service by requiring clients to provide a client certificate through the mTLS authentication protocol. Customers could also revoke or disable a client certificate, after which it would no longer be able to be used to authenticate a party initiating an encrypted session via mTLS.

When Cloudflare receives traffic from an end user, a service at the edge is responsible for terminating the incoming TLS connection. From there, this service is a reverse proxy, and it is responsible for acting as a bridge between the end user and various upstreams. Upstreams might include other services within Cloudflare such as Workers or Caching, or may travel through Cloudflare to an external server such as an origin hosting content. Sometimes, you may want to restrict access to an endpoint, ensuring that only authorized actors can access it. Using client certificates is a common way of authenticating users. This is referred to as mutual TLS, because both the server and client provide a certificate. When mTLS is enabled for a specific hostname, this service at the edge is responsible for parsing the incoming client certificate and converting that into metadata that is attached to HTTP requests that are forwarded to upstreams. The upstreams can process this metadata and make the decision whether the client is authorized or not.

mTLS client certificate revocation vulnerability with TLS Session Resumption

Customers can use the Cloudflare dashboard to revoke existing client certificates. Instead of immediately failing handshakes involving revoked client certificates, revocation is optionally enforced via Firewall Rules, which take effect at the HTTP request level. This leaves the decision to enforce revocation with the customer.

So how exactly does this service determine whether a client certificate is revoked?

When we see a client certificate presented as part of the TLS handshake, we store the entire certificate chain on the TLS connection. This means that for every HTTP request that is sent on the connection, the client certificate chain is available to the application. When we receive a request, we look at the following fields related to a client certificate chain:

  1. Leaf certificate Subject Key Identifier (SKI)
  2. Leaf certificate Serial Number (SN)
  3. Issuer certificate SKI
  4. Issuer certificate SN

Some of these values are used for upstream processing, but the issuer SKI and leaf certificate SN are used to query our internal data stores for revocation status. The data store indexes on an issuer SKI, and stores a collection of revoked leaf certificate serial numbers. If we find the leaf certificate in this collection, we set the relevant metadata for consumption in Firewall Rules.

But what does this have to do with TLS session resumption?

To explain this, let’s first discuss how session resumption works. At a high level, session resumption grants the ability for clients and servers to expedite the handshake process, saving both time and resources. The idea is that if a client and server successfully handshake, then future handshakes are more or less redundant, assuming nothing about the handshake needs to change at a fundamental level (e.g. cipher suite or TLS version).

Traditionally, there are two mechanisms for session resumption – session IDs and session tickets. In both cases, the TLS server will handle encrypting the context of the session, which is basically a snapshot of the acquired TLS state that is built up during the handshake process. Session IDs work in a stateful fashion, meaning that the server is responsible for saving this state, somewhere, and keying against the session ID. When a client provides a session ID in the client hello, the server checks to see if it has a corresponding session cached. If it does, then the handshake process is expedited and the cached session is restored. In contrast, session tickets work in a stateless fashion, meaning that the server has no need to store the encrypted session context. Instead, the server sends the client the encrypted session context (AKA a session ticket). In future handshakes, the client can send the session ticket in the client hello, which the server can decrypt in order to restore the session and expedite the handshake.

Recall that when a client presents a certificate, we store the certificate chain on the TLS connection. It was discovered that when sessions were resumed, the code to store the client certificate chain in application data did not run. As a result, we were left with an empty certificate chain, meaning we were unable to check the revocation status and pass this information to firewall rules for further processing.

To illustrate this, let’s use an example where mTLS is used for api.example.com. Firewall Rules are configured to block revoked certificates, and all certificates are revoked. We can reconstruct the client certificate checking behavior using a two-step process. First we use OpenSSL’s s_client to perform a handshake using the revoked certificate (recall that revocation has nothing to do with the success of the handshake – it only affects HTTP requests on the connection), and dump the session’s context into a “session.txt” file. We then issue an HTTP request on the connection, which fails with a 403 status code response because the certificate is revoked.

❯ echo -e "GET / HTTP/1.1\r\nHost:api.example.com\r\n\r\n" | openssl s_client -connect api.example.com:443 -cert cert2.pem -key key2.pem -ign_eof  -sess_out session.txt | grep 'HTTP/1.1'
depth=2 C=IE, O=Baltimore, OU=CyberTrust, CN=Baltimore CyberTrust Root
verify return:1
depth=1 C=US, O=Cloudflare, Inc., CN=Cloudflare Inc ECC CA-3
verify return:1
depth=0 C=US, ST=California, L=San Francisco, O=Cloudflare, Inc., CN=sni.cloudflaressl.com
verify return:1
HTTP/1.1 403 Forbidden
^C⏎

Now, if we reuse “session.txt” to perform session resumption and then issue an identical HTTP request, the request succeeds. This shouldn’t happen. We should fail both requests because they both use the same revoked client certificate.

❯ echo -e "GET / HTTP/1.1\r\nHost:api.example.com\r\n\r\n" | openssl s_client -connect api.example.com:443 -cert cert2.pem -key key2.pem -ign_eof -sess_in session.txt | grep 'HTTP/1.1'
HTTP/1.1 200 OK

How we addressed the problem

Upon realizing that session resumption led to the inability to properly check revocation status, our first reaction was to disable session resumption for all mTLS connections. This blocked the vulnerability immediately.

The next step was to figure out how to safely re-enable resumption for mTLS. To do so, we need to remove the requirement of depending on data stored within the TLS connection state. Instead, we can use an API call that will grant us access to the leaf certificate in both session resumption and non session resumption cases. Two pieces of information are necessary: the leaf certificate serial number and the issuer SKI. The issuer SKI is actually included in the leaf certificate, also known as the Authority Key Identifier (AKI). Similar to how one would obtain the SKI for a certificate, X509_get0_subject_key_id, we can use X509_get0_authority_key_id to get the AKI.

Detailed timeline

All timestamps are in UTC

In March 2021 we introduced a new feature in Firewall Rules that allows customers to block traffic from revoked mTLS certificates.

2022-12-16 21:53 – Cloudflare discovers that the vulnerability resulted from a bug whereby certificate revocation status was not checked for session resumptions. Cloudflare begins working on a fix to disable session resumption for all mTLS connections to the edge.
2022-12-17 02:20 – Cloudflare validates the fix and starts to roll out a fix globally.
2022-12-17 21:07 – Rollout is complete, mitigating the vulnerability.
2023-01-12 16:40 – Cloudflare starts to roll out a fix that supports both session resumption and revocation.
2023-01-18 14:07 – Rollout is complete.

In conclusion: once Cloudflare identified the vulnerability, a remediation was put into place quickly. A fix that correctly supports session resumption and revocation has been fully rolled out as of 2023-01-18. After reviewing the logs, Cloudflare has not seen any evidence that this vulnerability has been exploited in the wild.

Automate the deployment of an NGINX web service using Amazon ECS with TLS offload in CloudHSM

Post Syndicated from Nikolas Nikravesh original https://aws.amazon.com/blogs/security/automate-the-deployment-of-an-nginx-web-service-using-amazon-ecs-with-tls-offload-in-cloudhsm/

Customers who require private keys for their TLS certificates to be stored in FIPS 140-2 Level 3 certified hardware security modules (HSMs) can use AWS CloudHSM to store their keys for websites hosted in the cloud. In this blog post, we will show you how to automate the deployment of a web application using NGINX in AWS Fargate, with full integration with CloudHSM. You will also use AWS CodeDeploy to manage the deployment of changes to your Amazon Elastic Container Service (Amazon ECS) service.

CloudHSM offers FIPS 140-2 Level 3 HSMs that you can integrate with NGINX or Apache HTTP Server through the OpenSSL Dynamic Engine. The CloudHSM Client SDK 5 includes the OpenSSL Dynamic Engine to allow your web server to use a private key stored in the HSM with TLS versions 1.2 and 1.3 to support applications that are required to use FIPS 140-2 Level 3 validated HSMs.

CloudHSM uses the private key in the HSM as part of the server verification step of the TLS handshake that occurs every time that a new HTTPS connection is established between the client and server. Using the exchanged symmetric key, OpenSSL software performs the key exchange and bulk encryption. For more information about this process and how CloudHSM fits in, see How SSL/TLS offload with AWS CloudHSM works.

Solution overview

This blog post uses the AWS Cloud Development Kit (AWS CDK) to deploy the solution infrastructure. The AWS CDK allows you to define your cloud application resources using familiar programming languages.

Figure 1 shows an overview of the overall architecture deployed in this blog. This solution contains three CDK stacks: The TlsOffloadContainerBuildStack CDK stack deploys the CodeCommit, CodeBuild, and AmazonECR resources. The TlsOffloadEcsServiceStack CDK stack deploys the ECS Fargate service along with the required VPC resources. The TlsOffloadPipelineStack CDK stack deploys the CodePipeline resources to automate deployments of changes to the service configuration.

Figure 1: Overall architecture

Figure 1: Overall architecture

At a high level, here’s how the solution in Figure 1 works:

  1. Clients make an HTTPS request to the public IP address exposed by Network Load Balancer to connect to the web server and establish a secure connection that uses TLS.
  2. Network Load Balancer routes the request to one of the ECS hosts running in private virtual private cloud (VPC) subnets, which are connected to the CloudHSM cluster.
  3. The NGINX web server that is running on ECS containers performs a TLS handshake by using the private key stored in the HSM to establish a secure connection with the requestor.

Note: Although we don’t focus on perimeter protection in this post, AWS has a number of services that help provide layered perimeter protection for your internet-facing applications, such as AWS Shield and AWS WAF.

Figure 2 shows an overview of the automation infrastructure that is deployed by the TlsOffloadContainerBuildStack and TlsOffloadPipelineStack CDK stacks.

Figure 2: Deployment pipeline

Figure 2: Deployment pipeline

At a high level, here’s how the solution in Figure 2 works:

  1. A developer makes changes to the service configuration and commits the changes to the AWS CodeCommit repository.
  2. AWS CodePipeline detects the changes and invokes AWS CodeBuild to build a new version of the Docker image that is used in Amazon ECS.
  3. CodeBuild builds a new Docker image and publishes it to the Amazon Elastic Container Registry (Amazon ECR) repository.
  4. AWS CodeDeploy creates a new revision of the ECS task definition for the Amazon ECS service and initiates a deployment of the new service.

Required services

To build this architecture in your account, you need to use a role within your account that can configure the following services and features:

Prerequisites

To follow this walkthrough, you need to have the following components in place:

Step 1: Store secrets in Secrets Manager

As with other container projects, you need to decide what to build statically into the container (for example, libraries, code, or packages) and what to set as runtime parameters, to be pulled from a parameter store. In this walkthrough, we use Secrets Manager to store sensitive parameters and use the integration of Amazon ECS with Secrets Manager to securely retrieve them when the container is launched.

Important: You need to store the following information in Secrets Manager as plaintext, not as key/value pairs.

To create a new secret

  1. Open the Secrets Manager console and choose Store a new secret.
  2. On the Choose secret type page, do the following:
    1. For Secret type, choose Other type of secret.
    2. In Key/value pairs, choose Plaintext and enter your secret just as you would need it in your application.

The following is a list of the required secrets for this solution and how they look in the Secrets Manager console.

  • Your cluster-issuing certificate – this is the certificate that corresponds to the private key that you used to sign the cluster’s certificate signing request. In this example, the name of the secret for the certificate is tls/clustercert.
    Figure 3: Store the cluster certificate

    Figure 3: Store the cluster certificate

  • The web server certificate – In this example, the name of the secret for the web server certificate is tls/servercert. It will look similar to the following:
    Figure 4: Store the web server certificate

    Figure 4: Store the web server certificate

  • The fake PEM file for the private key stored in the HSM that you generated in the Prerequisites section. In this example, the name of the secret for the fake PEM file is tls/fakepem.
    Figure 5: Store the fake PEM

    Figure 5: Store the fake PEM

  • The HSM pin used to authenticate with the HSMs in your cluster. In this example, the name of the secret for the HSM pin is tls/pin.
    Figure 6: Store the HSM pin

    Figure 6: Store the HSM pin

After you’ve stored your secrets, you should see output similar to the following:

Figure 7: List of required secrets

Figure 7: List of required secrets

Step 2: Download and configure the CDK app

This post uses the AWS CDK to deploy the solution infrastructure. In this section, you will download the CDK app and configure it.

To download and configure the CDK app

  1. In your CDK environment that you created in the Prerequisites section, check out the source code from the aws-cloudhsm-tls-offload-blog GitHub repository. 
    git clone https://github.com/aws-samples/aws-cloudhsm-tls-offload-blog.git

  2. Edit the app_config.json file and update the <placeholder values> with your target configuration: 
    {
    "applicationAccount": "<AWS_ACCOUNT_ID>",
    "applicationRegion": "<REGION>",
    "networkConfig": {
        "vpcId": "<VPC_ID>",
        "publicSubnets": ["<PUBLIC_SUBNET_1>", "<PUBLIC_SUBNET_2>", ...],
        "privateSubnets": ["<PRIVATE_SUBNET_1>", "<PRIVATE_SUBNET_2>", ...]
    },
    "secrets": {
        "cloudHsmPin": "arn:aws:secretsmanager:<REGION>:<AWS_ACCOUNT_ID>:secret:<SECRET_ID>",
        "fakePem": "arn:aws:secretsmanager:<REGION>:<AWS_ACCOUNT_ID>:secret:<SECRET_ID>",
        "serverCert": "arn:aws:secretsmanager:<REGION>:<AWS_ACCOUNT_ID>:secret:<SECRET_ID>",
        "clusterCert": "arn:aws:secretsmanager:<REGION>:<AWS_ACCOUNT_ID>:secret:<SECRET_ID>"
    },
    "cloudhsm": {
        "clusterId": "<CLUSTER_ID>",
        "clusterSecurityGroup": "<CLUSTER_SECURITY_GROUP>"
    }
}

  3. Run the following command to build the CDK stacks from the root of the project directory. 
    npm run build

  4. To view the stacks that are available to deploy, run the following command from the root of the project directory. 
    cdk ls

    You should see the following stacks available to deploy:

    • TlsOffloadContainerBuildStack — Deploys the CodeCommit, CodeBuild, and ECR repository that builds the ECS container image.
    • TlsOffloadEcsServiceStack — Deploys the ECS Fargate service along with the required VPC resources.
    • TlsOffloadPipelineStack — Deploys the CodePipeline that automates the deployment of updates to the service.

Step 3: Deploy the container build stack

In this step, you will deploy the container build stack, and then create a build and verify that the image was built successfully.

To deploy the container build stack

Deploy the TlsOffloadContainerBuildStack stack that we described in Figure 2 to your AWS account. In your CDK environment, run the following command:

cdk deploy TlsOffloadContainerBuildStack

The command line interface (CLI) will prompt you to approve the changes. After you approve them, you will see the following resources deployed to your newly created CodeCommit repository.

  • Dockerfile — This file provides a containerized environment for each of the Fargate containers to run. It downloads and installs necessary dependencies to run the NGINX web server with CloudHSM.
  • nginx.conf — This file provides NGINX with the configuration settings to run an HTTPS web server with CloudHSM configured as the SSL engine that performs the TLS handshake. The following nginx.conf values have already been configured in the file; if you want to make changes, update the file before deployment:
    • ssl_engine is set to cloudhsm
    • the environment variable is env CLOUDHSM_PIN
    • error_log is set to stderr so that the Fargate container can capture the logs in CloudWatch
    • the server section is set up to listen on port 443
    • ssl_ciphers are configured for a server with an RSA private key
  • run.sh — This script configures the CloudHSM OpenSSL Dynamic Engine on the Fargate task before the NGINX server is started.
  • nginx.service — This file specifies the configuration settings that systemd uses to run the NGINX service. Included in this file is a reference to the file that contains the environment variables for the NGINX service. This provides the HSM pin to the OpenSSL Engine.
  • index.html — This file is a sample HTML file that is displayed when you navigate to the HTTPS endpoint of the load balancer in your browser.
  • dhparam.pem — This file provides sample Diffie-Hellman parameters for demonstration purposes, but AWS recommends that you generate your own. You can generate your own Diffie-Hellman parameters by running the following command with the OpenSSL CLI. These parameters are not required for TLS but are recommended to provide perfect forward secrecy in your encrypted messages. 
    openssl dhparam -out ./dhparam.pem 2048

Your repository should look like the following:

Figure 8: CodeCommit repository

Figure 8: CodeCommit repository

Before you deploy the Amazon ECS service, you need to build your first Docker image to populate the ECR repository. To successfully deploy the service, you need to have at least one image already present in the repository.

To create a build and verify the image was built successfully

  1. Open the AWS CodeBuild console.
  2. Find the CodeBuild project that was created by the CDK deployment and select it.
  3. Choose Start Build to initiate a new build.
  4. Wait for the build to complete successfully, and then open the Amazon ECR console.
  5. Select the repository that the CDK deployment created.

You should now see an image in your repository, similar to the following:

Figure 9: ECR repository

Figure 9: ECR repository

Step 4: Deploy the Amazon ECS service

Now that you have successfully built an ECR image, you can deploy the Amazon ECS service. This step deploys the following resources to your account:

  • VPC endpoints for the required AWS services that your ECS task needs to communicate with, including the following:
    • Amazon ECR
    • Secrets Manager
    • CloudWatch
    • CloudHSM
  • Network Load Balancer, which load balances HTTPS traffic to your ECS tasks.
  • A CloudWatch Logs log group to host the logs for the ECS tasks.
  • An ECS cluster with ECS tasks using your previously built Docker image that hosts the NGINX service.

To deploy the Amazon ECS service with the CDK

  • In your CDK environment, run the following command: 
    cdk deploy TlsOffloadEcsServiceStack

The CLI will prompt you to approve the changes. After you approve them, you will see these resources deploy to your account.

Checkpoint

At this point, you should have a working service. To confirm that you do, in your browser, navigate using HTTPS to the public address associated with the Network Load Balancer. While not covered in this blog, you can additionally configure DNS routing using Amazon Route53 to setup a custom domain name for your web service. You should see a screen similar to the following.

Figure 10: The sample website

Figure 10: The sample website

Step 5: Use CodePipeline to automate the deployment of changes to the web server

Now that you have deployed a preliminary version of the application, you can take a few steps to automate further releases of the web server. As you maintain this application in production, you might need to update one or more of the following items:

  • Your website HTML source and other required libraries (for example, CSS or JavaScript)
  • Your Docker environment, such as the OpenSSL libraries, operating system and CloudHSM packages, and NGINX version.
  • Re-deploy the service after rotating your web server private key and certificate in Secrets Manager

Next, you will set up a CodePipeline project that orchestrates the end-to-end deployment of a change to the application—from an update to the code in our CodeCommit repo to the deployment of updated container images and the redirection of user traffic by the load balancer to the updated application.

This step deploys to your account a deployment pipeline that connects your CodeCommit, CodeBuild, and Amazon ECS services.

Deploy the CodePipeline stack with CDK

In your CDK environment, run the following command:

cdk deploy TlsOffloadPipelineStack

The CLI will prompt you to approve the changes. After you approve them, you will see the resources deploy to your account.

Start a deployment

To verify that your automation is working correctly, start a new deployment in your CodePipeline by making a change to your source repository. If everything works, the CodeBuild project will build the latest version of the Dockerfile located in your CodeCommit repository and push it to Amazon ECR. Then, the CodeDeploy application will create a new version of the ECS task definition and deploy new tasks while spinning down the existing tasks.

View your website

Now that the deployment is complete, you should again be able to view your website in your browser by navigating to the website for your application. If you made changes to the source code, such as changes to your index.html file, you should see these changes now.

Verify that the web server is properly configured by checking that the website’s certificate matches the one that you created in the Prerequisites section. Figure 11 shows an example of a certificate.

Figure 11: Certificate for the application

Figure 11: Certificate for the application

To verify that your NGINX service is using your CloudHSM cluster to offload the TLS handshake, you can view the CloudHSM client logs for this application in CloudWatch in the log group that you specified when you configured the ECS task definition.

To view your CloudHSM client logs in CloudWatch

  1. Open the CloudWatch console.
  2. In the navigation pane, select Log Groups.
  3. Select the log group that was created for you by the CDK deployment.
  4. Select a log stream entry. Each log stream corresponds to an ECS instance that is running the NGINX web server.
  5. You should see the client logs for this instance, which will look similar to the following:
    Figure 12: Fargate task logs

    Figure 12: Fargate task logs

You can also verify your HSM connectivity by viewing your HSM audit logs.

To view your HSM audit logs

  1. Open the CloudWatch console.
  2. In the navigation pane, select Log Groups.
  3. Select the log group corresponding to your CloudHSM cluster. The log group has the following format: /aws/cloudhsm/<cluster-id>.
  4. You can see entries similar to the following, which indicates that the NGINX application is connecting and logging in to the HSM to perform cryptographic operations. 
    Time: 02/04/23 17:45:40.333033, usecs:1675532740333033
Version No : 1.0
Sequence No : 0x2
Reboot counter : 0x8
Opcode : CN_LOGIN (0xd)
Command Type(hex) : CN_MGMT_CMD (0x0)
User id : 3
Session Handle : 0x15010002
Response : 0x0:HSM Return: SUCCESS
Log type : USER_AUTH_LOG (2)
User Name : crypto_user
User Type : CN_CRYPTO_USER (1)

Conclusion

In this post, you learned how to set up a NGINX web server on Fargate in a secure, private subnet that offloads the TLS termination to a FIPS 140-2 Level 3 HSM environment that uses the CloudHSM OpenSSL Dynamic Engine. You also learned how to set up a deployment pipeline to automate the Fargate deployments when updates are made.

You can expand this solution to fit your individual use case. For example, you can use the NGINX web server as a reverse proxy for additional servers in your internal network, and set up mutual TLS between these internal servers.

Further reading

If you have feedback about this post, submit comments in the Comments section below. If you have questions about this post, start a new thread on the AWS CloudHSM re:Post or contact AWS Support.

Want more AWS Security news? Follow us on Twitter.

Alket Memushaj

Alket Memushaj

Alket Memushaj is a Principal Solutions Architect in the Market Development team for Capital Markets at AWS. In his role, Alket helps customers transform their business with the power of the AWS Cloud. His main focus is on helping customers deploy data and analytics, risk management, and electronic trading platforms in AWS. Alket previously led engineering teams at Morgan Stanley and consulted for global financial services at VMware.

Nikolas Nikravesh

Nikolas Nikravesh

Nikolas is a Software Development Engineer at AWS CloudHSM. He works with the SDK team to develop standards compliant SDKs and integrations to enable AWS customers to develop secure applications with CloudHSM.

Brad Woodward

Brad Woodward

Brad is a Senior Customer Delivery Architect with AWS Professional Services. Brad has presented at RSA and DefCon Skytalks, been an instructor at BlackHat and BlackHat Europe, presented tools at BlackHat Arsenal, and is the maintainer of several open source tools and platforms.

Out now! Auto-renew TLS certifications with DCV Delegation

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/introducing-dcv-delegation/

Out now! Auto-renew TLS certifications with DCV Delegation

Out now! Auto-renew TLS certifications with DCV Delegation

To get a TLS certificate issued, the requesting party must prove that they own the domain through a process called Domain Control Validation (DCV). As industry wide standards have evolved to enhance security measures, this process has become manual for Cloudflare customers that manage their DNS externally. Today, we’re excited to announce DCV Delegation — a feature that gives all customers the ability offload the DCV process to Cloudflare, so that all certificates can be auto-renewed without the management overhead.

Security is of utmost importance when it comes to managing web traffic, and one of the most critical aspects of security is ensuring that your application always has a TLS certificate that’s valid and up-to-date. Renewing TLS certificates can be an arduous and time-consuming task, especially as the recommended certificate lifecycle continues to gradually decrease, causing certificates to be renewed more frequently. Failure to get a certificate renewed can result in downtime or insecure connection which can lead to revenue decrease, mis-trust with your customers, and a management nightmare for your Ops team.

Every time a certificate is renewed with a Certificate Authority (CA), the certificate needs to pass a check called Domain Control Validation (DCV). This is a process that a CA goes through to verify that the party requesting the certificate does in fact own or control ownership over the domain for which the certificate is being requested. One of the benefits of using Cloudflare as your Authoritative DNS provider is that we can always prove ownership of your domain and therefore auto-renew your certificates. However, a big chunk of our customers manage their DNS externally. Before today, certificate renewals required these customers to make manual changes every time the certificate came up for renewal. Now, with DCV Delegation – you can let Cloudflare do all the heavy lifting.

DCV primer

Before we dive into how DCV Delegation works, let’s talk about it. DCV is the process of verifying that the party requesting a certificate owns or controls the domain for which they are requesting a certificate.

Out now! Auto-renew TLS certifications with DCV Delegation

When a subscriber requests a certificate from a CA, the CA returns validation tokens that the domain owner needs to place. The token can be an HTTP file that the domain owner needs to serve from a specific endpoint or it can be a DNS TXT record that they can place at their Authoritative DNS provider. Once the tokens are placed, ownership has been proved, and the CA can proceed with the certificate issuance.

Better security practices for certificate issuance

Certificate issuance is a serious process. Any shortcomings can lead to a malicious actor issuing a certificate for a domain they do not own. What this means is that the actor could serve the certificate from a spoofed domain that looks exactly like yours and hijack and decrypt the incoming traffic. Because of this, over the last few years, changes have been put in place to ensure higher security standards for certificate issuances.

Shorter certificate lifetimes

The first change is the move to shorter lived certificates. Before 2011, a certificate could be valid for up to 96 months (about eight years). Over the last few years, the accepted validity period has been significantly shortened. In 2012, certificate validity went down to 60 months (5 years), in 2015 the lifespan was shortened to 39 months (about 3 years), in 2018 to 24 months (2 years), and in 2020, the lifetime was dropped to 13 months. Following the trend, we’re going to continue to see certificate lifetimes decrease even further to 3 month certificates as the standard. We’re already seeing this in action with Certificate Authorities like Let’s Encrypt and Google Trust Services offering a maximum validity period of 90 days (3 months). Shorter-lived certificates are aimed to reduce the compromise window in a situation where a malicious party has gained control over a TLS certificate or private key. The shorter the lifetime, the less time the bad actor can make use of the compromised material. At Cloudflare, we even give customers the ability to issue 2 week certificates to reduce the impact window even further.

While this provides a better security posture, it does require more overhead management for the domain owner, as they’ll now be responsible for completing the DCV process every time the certificate is up for renewal, which can be every 90 days. In the past, CAs would allow the re-use of validation tokens, meaning even if the certificate was renewed more frequently, the validation tokens could be re-used so that the domain owner wouldn’t need to complete DCV again. Now, more and more CAs are requiring unique tokens to be placed for every renewal, meaning shorter certificate lifetimes now result in additional management overhead.

Wildcard certificates now require DNS-based DCV

Aside from certificate lifetimes, the process required to get a certificate issued has developed stricter requirements over the last few years. The Certificate Authority/Browser Forum (CA/B Forum), the governing body that sets the rules and standards for certificates, has enforced or stricter requirements around certificate issuance to ensure that certificates are issued in a secure manner that prevents a malicious actor from obtaining certificates for domains they do not own.

In May 2021, the CA/B Forum voted to require DNS based validation for any certificate with a wildcard certificate on it. Meaning, that if you would like to get a TLS certificate that covers example.com and *.example.com, you can no longer use HTTP based validation, but instead, you will need to add TXT validation tokens to your DNS provider to get that certificate issued. This is because a wildcard certificate covers a large portion of the domain’s namespace. If a malicious actor receives a certificate for a wildcard hostname, they now have control over all of the subdomains under the domain. Since HTTP validation only proves ownership of a hostname and not the whole domain, it’s better to use DNS based validation for a certificate with broader coverage.

All of these changes are great from a security standpoint – we should be adopting these processes! However, this also requires domain owners to adapt to the changes. Failure to do so can lead to a certificate renewal failure and downtime for your application. If you’re managing more than 10 domains, these new processes become a management nightmare fairly quickly.

At Cloudflare, we’re here to help. We don’t think that security should come at the cost of reliability or the time that your team spends managing new standards and requirements. Instead, we want to make it as easy as possible for you to have the best security posture for your certificates, without the management overhead.

How Cloudflare helps customers auto-renew certificates

Out now! Auto-renew TLS certifications with DCV Delegation

For years, Cloudflare has been managing TLS certificates for 10s of millions of domains. One of the reasons customers choose to manage their TLS certificates with Cloudflare is that we keep up with all the changes in standards, so you don’t have to.

One of the superpowers of having Cloudflare as your Authoritative DNS provider is that Cloudflare can add necessary DNS records on your behalf to ensure successful certificate issuances. If you’re using Cloudflare for your DNS, you probably haven’t thought about certificate renewals, because you never had to. We do all the work for you.

When the CA/B Forum announced that wildcard certificates would now require TXT based validation to be used, customers that use our Authoritative DNS didn’t even notice any difference – we continued to do the auto-renewals for them, without any additional work on their part.

While this provides a reliability and management boost to some customers, it still leaves out a large portion of our customer base — customers who use Cloudflare for certificate issuance with an external DNS provider.

There are two groups of customers that were impacted by the wildcard DCV change: customers with domains that host DNS externally – we call these “partial” zones – and SaaS providers that use Cloudflare’s SSL for SaaS product to provide wildcard certificates for their customers’ domains.

Customers with “partial” domains that use wildcard certificates on Cloudflare are now required to fetch the TXT DCV tokens every time the certificate is up for renewal and manually place those tokens at their DNS provider. With Cloudflare deprecating DigiCert as a Certificate Authority, certificates will now have a lifetime of 90 days, meaning this manual process will need to occur every 90 days for any certificate with a wildcard hostname.

Customers that use our SSL for SaaS product can request that Cloudflare issues a certificate for their customer’s domain – called a custom hostname. SaaS providers on the Enterprise plan have the ability to extend this support to wildcard custom hostnames, meaning we’ll issue a certificate for the domain (example.com) and for a wildcard (*.example.com). The issue with that is that SaaS providers will now be required to fetch the TXT DCV tokens, return them to their customers so that they can place them at their DNS provider, and do this process every 90 days. Supporting this requires a big change to our SaaS provider’s management system.

At Cloudflare, we want to help every customer choose security, reliability, and ease of use — all three! And that’s where DCV Delegation comes in.

Enter DCV Delegation: certificate auto-renewal for every Cloudflare customer

DCV Delegation is a new feature that allows customers who manage their DNS externally to delegate the DCV process to Cloudflare. DCV Delegation requires customers to place a one-time record that allows Cloudflare to auto-renew all future certificate orders, so that there’s no manual intervention from the customer at the time of the renewal.

How does it work?

Customers will now be able to place a CNAME record at their Authoritative DNS provider at their acme-challenge endpoint – where the DCV records are currently placed – to point to a domain on Cloudflare.

This record will have the the following syntax:

_acme-challenge.<domain.TLD> CNAME <domain.TLD>.<UUID>.dcv.cloudflare.com

Let’s say I own example.com and need to get a certificate issued for it that covers the apex and wildcard record. I would place the following record at my DNS provider: _acme-challenge.example.com CNAME example.com.<UUID>.dcv.cloudflare.com. Then, Cloudflare would place the two TXT DNS records required to issue the certificate at  example.com.<UUID>.dcv.cloudflare.com.

As long as the partial zone or custom hostname remains Active on Cloudflare, Cloudflare will add the DCV tokens on every renewal. All you have to do is keep the CNAME record in place.

If you’re a “partial” zone customer or an SSL for SaaS customer, you will now see this card in the dashboard with more information on how to use DCV Delegation, or you can read our documentation to learn more.

DCV Delegation for Partial Zones:

Out now! Auto-renew TLS certifications with DCV Delegation

DCV Delegation for Custom Hostnames:

Out now! Auto-renew TLS certifications with DCV Delegation

The UUID in the CNAME target is a unique identifier. Each partial domain will have its own UUID that corresponds to all of the DCV delegation records created under that domain. Similarly, each SaaS zone will have one UUID that all custom hostnames under that domain will use. Keep in mind that if the same domain is moved to another account, the UUID value will change and the corresponding DCV delegation records will need to be updated.

If you’re using Cloudflare as your Authoritative DNS provider, you don’t need to worry about this! We already add the DCV tokens on your behalf to ensure successful certificate renewals.

What’s next?

Right now, DCV Delegation only allows delegation to one provider. That means that if you’re using multiple CDN providers or you’re using Cloudflare to manage your certificates but you’re also issuing certificates for the same hostname for your origin server then DCV Delegation won’t work for you. This is because once that CNAME record is pointed to Cloudflare, only Cloudflare will be able to add DCV tokens at that endpoint, blocking you or an external CDN provider from doing the same.

However, an RFC draft is in progress that will allow each provider to have a separate “acme-challenge” endpoint, based on the ACME account used to issue the certs. Once this becomes standardized and CAs and CDNs support it, customers will be able to use multiple providers for DCV delegation.

In conclusion, DCV delegation is a powerful feature that simplifies the process of managing certificate renewals for all Cloudflare customers. It eliminates the headache of managing certificate renewals, ensures that certificates are always up-to-date, and most importantly, ensures that your web traffic is always secure. Try DCV delegation today and see the difference it can make for your web traffic!

Mutual TLS now available for Workers

Post Syndicated from Tanushree Sharma original https://blog.cloudflare.com/mtls-workers/

Mutual TLS now available for Workers

Mutual TLS now available for Workers

In today’s digital world, security is a top priority for businesses. Whether you’re a Fortune 500 company or a startup just taking off, it’s essential to implement security measures in order to protect sensitive information. Security starts inside an organization; it starts with having Zero Trust principles that protect access to resources.

Mutual TLS (mTLS) is useful in a Zero Trust world to secure a wide range of network services and applications: APIs, web applications, microservices, databases and IoT devices. Cloudflare has products that enforce mTLS: API Shield uses it to secure API endpoints and Cloudflare Access uses it to secure applications. Now, with mTLS support for Workers you can use Workers to authenticate to services secured by mTLS directly. mTLS for Workers is now generally available for all Workers customers!

A recap on how TLS works

Before diving into mTLS, let’s first understand what TLS (Transport Layer Security) is. Any website that uses HTTPS, like the one you’re reading this blog on, uses TLS encryption. TLS is used to create private communications on the Internet – it gives users assurance that the website you’re connecting to is legitimate and any information passed to it is encrypted.

TLS is enforced through a TLS handshake where the client and server exchange messages in order to create a secure connection. The handshake consists of several steps outlined below:

Mutual TLS now available for Workers

The client and server exchange cryptographic keys, the client authenticates the server’s identity and the client and server generate a secret key that’s used to create an encrypted connection.

For most connections over the public Internet TLS is sufficient. If you have a website, for example a landing page, storefront or documentation, you want any user to be able to navigate to it – validating the identity of the client isn’t necessary. But, if you have services that run on a corporate network or private/sensitive applications you may want access to be locked down to only authorized clients.

Enter mTLS

With mTLS, both the client and server present a digital certificate during the TLS handshake to mutually verify each other’s credentials and prove identities. mTLS adds additional steps to the TLS handshake in order to authenticate the client as well as the server.

In comparison to TLS, with mTLS the server also sends a ‘Certificate Request’ message that contains a list of parties that it trusts and it tells the client to respond with its certificate. The mTLS authentication process is outlined below:

Mutual TLS now available for Workers

mTLS is typically used when a managed list of clients (eg. users, devices) need access to a server. It uses cryptographically signed certificates for authentication, which are harder to spoof than passwords or tokens. Some common use cases include: communications between APIs or microservices, database connections from authorized hosts, and machine-to-machine IoT connections.

Introducing mTLS on Workers

With mTLS support on Workers, your Workers can now communicate with resources that enforce an mTLS connection. mTLS through Workers can be configured in just a few easy steps:

1. Upload a client certificate and private key obtained from your service that enforces mTLS using wrangler

wrangler mtls-certificate upload --cert cert.pem --key key.pem --name my-client-cert

2. Add a mtls_certificates binding in your project’s wrangler.toml file. The CERTIFICATE_ID is returned after your certificate is uploaded in step 1

mtls_certificates = [
 { binding = "MY_CERT", certificate_id = "<CERTIFICATE_ID>" }
]

3. Add the mTLS binding to any fetch() requests. This will present the client certificate when establishing the TLS connection.

index.js

export default {
   async fetch(request, environment) {
       return await environment.MY_CERT.fetch("https://example-secure-origin.com")
   }

}

To get per-request granularity, you can configure multiple mTLS certificates if you’re connecting to multiple hosts within the same Worker. There’s a limit of 1,000 certificates that can be uploaded per account. Contact your account team or reach out through the Cloudflare Developer Discord if you need more certificates.

Try it yourself

It’s that easy! For more information and to try it yourself, refer to our developer documentation – client authentication with mTLS.

We love to see what you’re developing on Workers. Join our Discord community and show us what you’re building!

Three ways to boost your email security and brand reputation with AWS

Post Syndicated from Michael Davie original https://aws.amazon.com/blogs/security/three-ways-to-boost-your-email-security-and-brand-reputation-with-aws/

If you own a domain that you use for email, you want to maintain the reputation and goodwill of your domain’s brand. Several industry-standard mechanisms can help prevent your domain from being used as part of a phishing attack. In this post, we’ll show you how to deploy three of these mechanisms, which visually authenticate emails sent from your domain to users and verify that emails are encrypted in transit. It can take as little as 15 minutes to deploy these mechanisms on Amazon Web Services (AWS), and the result can help to provide immediate and long-term improvements to your organization’s email security.

Phishing through email remains one of the most common ways that bad actors try to compromise computer systems. Incidents of phishing and related crimes far outnumber the incidents of other categories of internet crime, according to the most recent FBI Internet Crime Report. Phishing has consistently led to large annual financial losses in the US and globally.

Overview of BIMI, MTA-STS, and TLS reporting

An earlier post has covered how you can use Amazon Simple Email Service (Amazon SES) to send emails that align with best practices, including the IETF internet standards: Sender Policy Framework (SPF), DomainKeys Identified Mail (DKIM), and Domain-based Message Authentication, Reporting, and Conformance (DMARC). This post will show you how to build on this foundation and configure your domains to align with additional email security standards, including the following:

  • Brand Indicators for Message Identification (BIMI) – This standard allows you to associate a logo with your email domain, which some email clients will display to users in their inbox. Visit the BIMI Group’s Where is my BIMI Logo Displayed? webpage to see how logos are displayed in the user interfaces of BIMI-supporting mailbox providers; Figure 1 shows a mock-up of a typical layout that contains a logo.
  • Mail Transfer Agent Strict Transport Security (MTA-STS) – This standard helps ensure that email servers always use TLS encryption and certificate-based authentication when they send messages to your domain, to protect the confidentiality and integrity of email in transit.
  • SMTP TLS reporting – This reporting allows you to receive reports and monitor your domain’s TLS security posture, identify problems, and learn about attacks that might be occurring.
Figure 1: A mock-up of how BIMI enables branded logos to be displayed in email user interfaces

Figure 1: A mock-up of how BIMI enables branded logos to be displayed in email user interfaces

These three standards require your Domain Name System (DNS) to publish specific records, for example by using Amazon Route 53, that point to web pages that have additional information. You can host this information without having to maintain a web server by storing it in Amazon Simple Storage Service (Amazon S3) and delivering it through Amazon CloudFront, secured with a certificate provisioned from AWS Certificate Manager (ACM).

Note: This AWS solution works for DKIM, BIMI, and DMARC, regardless of what you use to serve the actual email for your domains, which services you use to send email, and where you host DNS. For purposes of clarity, this post assumes that you are using Route 53 for DNS. If you use a different DNS hosting provider, you will manually configure DNS records in your existing hosting provider.

Solution architecture

The architecture for this solution is depicted in Figure 2.

Figure 2: The architecture diagram showing how the solution components interact

Figure 2: The architecture diagram showing how the solution components interact

The interaction points are as follows:

  1. The web content is stored in an S3 bucket, and CloudFront has access to this bucket through an origin access identity, a mechanism of AWS Identity and Access Management (IAM).
  2. As described in more detail in the BIMI section of this blog post, the Verified Mark Certificate is obtained from a BIMI-qualified certificate authority and stored in the S3 bucket.
  3. When an external email system receives a message claiming to be from your domain, it looks up BIMI records for your domain in DNS. As depicted in the diagram, a DNS request is sent to Route 53.
  4. To retrieve the BIMI logo image and Verified Mark Certificate, the external email system will make HTTPS requests to a URL published in the BIMI DNS record. In this solution, the URL points to the CloudFront distribution, which has a TLS certificate provisioned with ACM.

A few important warnings

Email is a complex system of interoperating technologies. It is also brittle: a typo or a missing DNS record can make the difference between whether an email is delivered or not. Pay close attention to your email server and the users of your email systems when implementing the solution in this blog post. The main indicator that something is wrong is the absence of email. Instead of seeing an error in your email server’s log, users will tell you that they’re expecting to receive an email from somewhere and it’s not arriving. Or they will tell you that they sent an email, and their recipient can’t find it.

The DNS uses a lot of caching and time-out values to improve its efficiency. That makes DNS records slow and a little unpredictable as they propagate across the internet. So keep in mind that as you monitor your systems, it can be hours or even more than a day before the DNS record changes have an effect that you can detect.

This solution uses AWS Cloud Development Kit (CDK) custom resources, which are supported by AWS Lambda functions that will be created as part of the deployment. These functions are configured to use CDK-selected runtimes, which will eventually pass out of support and require you to update them.

Prerequisites

You will need permission in an AWS account to create and configure the following resources:

  • An Amazon S3 bucket to store the files and access logs
  • A CloudFront distribution to publicly deliver the files from the S3 bucket
  • A TLS certificate in ACM
  • An origin access identity in IAM that CloudFront will use to access files in Amazon S3
  • Lambda functions, IAM roles, and IAM policies created by CDK custom resources

You might also want to enable these optional services:

  • Amazon Route 53 for setting the necessary DNS records. If your domain is hosted by another DNS provider, you will set these DNS records manually.
  • Amazon SES or an Amazon WorkMail organization with a single mailbox. You can configure either service with a subdomain (for example, [email protected]) such that the existing domain is not disrupted, or you can create new email addresses by using your existing email mailbox provider.

BIMI has some additional requirements:

  • BIMI requires an email domain to have implemented a strong DMARC policy so that recipients can be confident in the authenticity of the branded logos. Your email domain must have a DMARC policy of p=quarantine or p=reject. Additionally, the domain’s policy cannot have sp=none or pct<100.

    Note: Do not adjust the DMARC policy of your domain without careful testing, because this can disrupt mail delivery.

  • You must have your brand’s logo in Scaled Vector Graphics (SVG) format that conforms to the BIMI standard. For more information, see Creating BIMI SVG Logo Files on the BIMI Group website.
  • Purchase a Verified Mark Certificate (VMC) issued by a third-party certificate authority. This certificate attests that the logo, organization, and domain are associated with each other, based on a legal trademark registration. Many email hosting providers require this additional certificate before they will show your branded logo to their users. Others do not currently support BIMI, and others might have alternative mechanisms to determine whether to show your logo. For more information about purchasing a Verified Mark Certificate, see the BIMI Group website.

    Note: If you are not ready to purchase a VMC, you can deploy this solution and validate that BIMI is correctly configured for your domain, but your branded logo will not display to recipients at major email providers.

What gets deployed in this solution?

This solution deploys the DNS records and supporting files that are required to implement BIMI, MTA-STS, and SMTP TLS reporting for an email domain. We’ll look at the deployment in more detail in the following sections.

BIMI

BIMI is described by the Internet Engineering Task Force (IETF) as follows:

Brand Indicators for Message Identification (BIMI) permits Domain Owners to coordinate with Mail User Agents (MUAs) to display brand-specific Indicators next to properly authenticated messages. There are two aspects of BIMI coordination: a scalable mechanism for Domain Owners to publish their desired Indicators, and a mechanism for Mail Transfer Agents (MTAs) to verify the authenticity of the Indicator. This document specifies how Domain Owners communicate their desired Indicators through the BIMI Assertion Record in DNS and how that record is to be interpreted by MTAs and MUAs. MUAs and mail-receiving organizations are free to define their own policies for making use of BIMI data and for Indicator display as they see fit.

If your organization has a trademark-protected logo, you can set up BIMI to have that logo displayed to recipients in their email inboxes. This can have a positive impact on your brand and indicates to end users that your email is more trustworthy. The BIMI Group shows examples of how brand logos are displayed in user inboxes, as well as a list of known email service providers that support the display of BIMI logos.

As a domain owner, you can implement BIMI by publishing the relevant DNS records and hosting the relevant files. To have your logo displayed by most email hosting providers, you will need to purchase a Verified Mark Certificate from a BIMI-qualified certificate authority.

This solution will deploy a valid BIMI record in Route 53 (or tell you what to publish in the DNS if you’re not using Route 53) and will store your provided SVG logo and Verified Mark Certificate files in Amazon S3, to be delivered through CloudFront with a valid TLS certificate from ACM.

To support BIMI, the solution makes the following changes to your resources:

  1. A DNS record of type TXT is published at the following host:
    default._bimi.<your-domain>. The value of this record is: v=BIMI1; l=<url-of-your-logo> a=<url-of-verified-mark-certificate>. The value of <your-domain> refers to the domain that is used in the From header of messages that your organization sends.
  2. The logo and optional Verified Mark Certificate are hosted publicly at the HTTPS locations defined by <url-of-your-logo> and <url-of-verified-mark-certificate>, respectively.

MTA-STS

MTA-STS is described by the IETF in RFC 8461 as follows:

SMTP (Simple Mail Transport Protocol) MTA Strict Transport Security (MTA-STS) is a mechanism enabling mail service providers to declare their ability to receive Transport Layer Security (TLS) secure SMTP connections and to specify whether sending SMTP servers should refuse to deliver to MX hosts that do not offer TLS with a trusted server certificate.

Put simply, MTA-STS helps ensure that email servers always use encryption and certificate-based authentication when sending email to your domains, so that message integrity and confidentiality are preserved while in transit across the internet. MTA-STS also helps to ensure that messages are only sent to authorized servers.

This solution will deploy a valid MTA-STS policy record in Route 53 (or tell you what value to publish in the DNS if you’re not using Route 53) and will create an MTA-STS policy document to be hosted on S3 and delivered through CloudFront with a valid TLS certificate from ACM.

To support MTA-STS, the solution makes the following changes to your resources:

  1. A DNS record of type TXT is published at the following host: _mta-sts.<your-domain>. The value of this record is: v=STSv1; id=<unique value used for cache invalidation>.
  2. The MTA-STS policy document is hosted at and obtained from the following location: https://mta-sts.<your-domain>/.well-known/mta-sts.txt.
  3. The value of <your-domain> in both cases is the domain that is used for routing inbound mail to your organization and is typically the same domain that is used in the From header of messages that your organization sends externally. Depending on the complexity of your organization, you might receive inbound mail for multiple domains, and you might choose to publish MTA-STS policies for each domain.

Is it ever bad to encrypt everything?

In the example MTA-STS policy file provided in the GitHub repository and explained later in this post, the MTA-STS policy mode is set to testing. This means that your email server is advertising its willingness to negotiate encrypted email connections, but it does not require TLS. Servers that want to send mail to you are allowed to connect and deliver mail even if there are problems in the TLS connection, as long as you’re in testing mode. You should expect reports when servers try to connect through TLS to your mail server and fail to do so.

Be fully prepared before you change the MTA-STS policy to enforce. After this policy is set to enforce, servers that follow the MTA-STS policy and that experience an enforceable TLS-related error when they try to connect to your mail server will not deliver mail to your mail server. This is a difficult situation to detect. You will simply stop receiving email from servers that comply with the policy. You might receive reports from them indicating what errors they encountered, but it is not guaranteed. Be sure that the email address you provide in SMTP TLS reporting (in the following section) is functional and monitored by people who can take action to fix issues. If you miss TLS failure reports, you probably won’t receive email. If the TLS certificate that you use on your email server expires, and your MTA-STS policy is set to enforce, this will become an urgent issue and will disrupt the flow of email until it is fixed.

SMTP TLS reporting

SMTP TLS reporting is described by the IETF in RFC 8460 as follows:

A number of protocols exist for establishing encrypted channels between SMTP Mail Transfer Agents (MTAs), including STARTTLS, DNS-Based Authentication of Named Entities (DANE) TLSA, and MTA Strict Transport Security (MTA-STS). These protocols can fail due to misconfiguration or active attack, leading to undelivered messages or delivery over unencrypted or unauthenticated channels. This document describes a reporting mechanism and format by which sending systems can share statistics and specific information about potential failures with recipient domains. Recipient domains can then use this information to both detect potential attacks and diagnose unintentional misconfigurations.

As you gain the security benefits of MTA-STS, SMTP TLS reporting will allow you to receive reports from other internet email providers. These reports contain information that is valuable when monitoring your TLS security posture, identifying problems, and learning about attacks that might be occurring.

This solution will deploy a valid SMTP TLS reporting record on Route 53 (or provide you with the value to publish in the DNS if you are not using Route 53).

To support SMTP TLS reporting, the solution makes the following changes to your resources:

  1. A DNS record of type TXT is published at the following host: _smtp._tls.<your-domain>. The value of this record is: v=TLSRPTv1; rua=mailto:<report-receiver-email-address>
  2. The value of <report-receiver-email-address> might be an address in your domain or in a third-party provider. Automated systems that process these reports must be capable of processing GZIP compressed files and parsing JSON.

Deploy the solution with the AWS CDK

In this section, you’ll learn how to deploy the solution to create the previously described AWS resources in your account.

  1. Clone the following GitHub repository:

    git clone https://github.com/aws-samples/serverless-mail
    cd serverless-mail/email-security-records

  2. Edit CONFIG.py to reflect your desired settings, as follows:
    1. If no Verified Mark Certificate is provided, set VMC_FILENAME = None.
    2. If your DNS zone is not hosted on Route 53, or if you do not want this app to manage Route 53 DNS records, set ROUTE_53_HOSTED = False. In this case, you will need to set TLS_CERTIFICATE_ARN to the Amazon Resource Name (ARN) of a certificate hosted on ACM in us-east-1. This certificate is used by CloudFront and must support two subdomains: mta-sts and your configured BIMI_ASSET_SUBDOMAIN.
  3. Finalize the preparation, as follows:
    1. Place your BIMI logo and Verified Mark Certificate files in the assets folder.
    2. Create an MTA-STS policy file at assets/.well-known/mta-sts.txt to reflect your mail exchange (MX) servers and policy requirements. An example file is provided at assets/.well-known/mta-sts.txt.example
  4. Deploy the solution, as follows:
    1. Open a terminal in the email-security-records folder.
    2. (Recommended) Create and activate a virtual environment by running the following commands.
      python3 -m venv .venv
      source .venv/bin/activate
    3. Install the Python requirements in your environment with the following command.
      pip install -r requirements.txt
    4. Assume a role in the target account that has the permissions outlined in the Prerequisites section of this post.

      Using AWS CDK version 2.17.0 or later, deploy the bootstrap in the target account by running the following command. To learn more, see Bootstrapping in the AWS CDK Developer Guide.
      cdk bootstrap

    5. Run the following command to synthesize the CloudFormation template. Review the output of this command to verify what will be deployed.
      cdk synth
    6. Run the following command to deploy the CloudFormation template. You will be prompted to accept the IAM changes that will be applied to your account.
      cdk deploy

      Note: If you use Route53, these records are created and activated in your DNS zones as soon as the CDK finishes deploying. As the records propagate through the DNS, they will gradually start affecting the email in the affected domains.

    7. If you’re not using Route53 and instead are using a third-party DNS provider, create the CNAME and TXT records as indicated. In this case, your email is not affected by this solution until you create the records in DNS.

Testing and troubleshooting

After you have deployed the CDK solution, you can test it to confirm that the DNS records and web resources are published correctly.

BIMI

  1. Query the BIMI DNS TXT record for your domain by using the dig or nslookup command in your terminal.

    dig +short TXT default._bimi.<your-domain.example>

    Verify the response. For example:

    "v=BIMI1; l=https://bimi-assets.<your-domain.example>/logo.svg"

  2. In your web browser, open the URL from that response (for example, https://bimi-assets.<your-domain.example>/logo.svg) to verify that the logo is available and that the HTTPS certificate is valid.
  3. The BIMI group provides a tool to validate your BIMI configuration. This tool will also validate your VMC if you have purchased one.

MTA-STS

  1. Query the MTA-STS DNS TXT record for your domain.

    dig +short TXT _mta-sts.<your-domain.example>

    The value of this record is as follows:

    v=STSv1; id=<unique value used for cache invalidation>

  2. You can load the MTA-STS policy document using your web browser. For example, https://mta-sts.<your-domain.example>/.well-known/mta-sts.txt
  3. You can also use third party tools to examine your MTA-STS configuration, such as MX Toolbox.

TLS reporting

  1. Query the TLS reporting DNS TXT record for your domain.

    dig +short TXT _smtp._tls.<your-domain.example>

    Verify the response. For example:

    "v=TLSRPTv1; rua=mailto:<your email address>"

  2. You can also use third party tools to examine your TLS reporting configuration, such as Easy DMARC.

Depending on which domains you communicate with on the internet, you will begin to see TLS reports arriving at the email address that you have defined in the TLS reporting DNS record. We recommend that you closely examine the TLS reports, and use automated analytical techniques over an extended period of time before changing the default testing value of your domain’s MTA-STS policy. Not every email provider will send TLS reports, but examining the reports in aggregate will give you a good perspective for making changes to your MTA-STS policy.

Cleanup

To remove the resources created by this solution:

  1. Open a terminal in the cdk-email-security-records folder.
  2. Assume a role in the target account with permission to delete resources.
  3. Run cdk destroy.

Note: The asset and log buckets are automatically emptied and deleted by the cdk destroy command.

Conclusion

When external systems send email to or receive email from your domains they will now query your new DNS records and will look up your domain’s BIMI, MTA-STS, and TLS reporting information from your new CloudFront distribution. By adopting the email domain security mechanisms outlined in this post, you can improve the overall security posture of your email environment, as well as the perception of your brand.

 
If you have feedback about this post, submit comments in the Comments section below. If you have questions about this post, contact AWS Support.

Want more AWS Security news? Follow us on Twitter.

Michael Davie

Michael Davie

Michael is a Senior Industry Specialist with AWS Security Assurance. He works with our customers, their regulators, and AWS teams to help raise the bar on secure cloud adoption and usage. Michael has over 20 years of experience working in the defence, intelligence, and technology sectors in Canada and is a licensed professional engineer.

Jesse Thompson

Jesse Thompson

Jesse is an Email Deliverability Manager with the Amazon Simple Email Service team. His background is in enterprise IT development and operations, with a focus on email abuse mitigation and encouragement of authenticity practices with open standard protocols. Jesse’s favorite activity outside of technology is recreational curling.

A new, configurable and scalable version of Geo Key Manager, now available in Closed Beta

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/configurable-and-scalable-geo-key-manager-closed-beta/

A new, configurable and scalable version of Geo Key Manager, now available in Closed Beta

A new, configurable and scalable version of Geo Key Manager, now available in Closed Beta

Today, traffic on the Internet stays encrypted through the use of public and private keys that encrypt the data as it’s being transmitted. Cloudflare helps secure millions of websites by managing the encryption keys that keep this data protected. To provide lightning fast services, Cloudflare stores these keys on our fleet of data centers that spans more than 150 countries. However, some compliance regulations require that private keys are only stored in specific geographic locations.

In 2017, we introduced Geo Key Manager, a product that allows customers to store and manage the encryption keys for their domains in different geographic locations so that compliance regulations are met and that data remains secure. We launched the product a few months before General Data Protection Regulation (GDPR) went into effect and built it to support three regions: the US, the European Union (EU), and a set of our top tier data centers that employ the highest security measures. Since then, GDPR-like laws have quickly expanded and now, more than 15 countries have comparable data protection laws or regulations that include restrictions on data transfer across and/or data localization within a certain boundary.

At Cloudflare, we like to be prepared for the future. We want to give our customers tools that allow them to maintain compliance in this ever-changing environment. That’s why we’re excited to announce a new version of Geo Key Manager — one that allows customers to define boundaries by country, ”only store my private keys in India”, by a region ”only store my private keys in the European Union”, or by a standard, such as “only store my private keys in FIPS compliant data centers” — now available in Closed Beta, sign up here!

Learnings from Geo Key Manager v1

Geo Key Manager has been around for a few years now, and we’ve used this time to gather feedback from our customers. As the demand for a more flexible system grew, we decided to go back to the drawing board and create a new version of Geo Key Manager that would better meet our customers’ needs.

We initially launched Geo Key Manager with support for US, EU, and Highest Security Data centers. Those regions were sufficient at the time, but customers wrestling with data localization obligations in other jurisdictions need more flexibility when it comes to selecting countries and regions. Some customers want to be able to set restrictions to maintain their private keys in one country, some want the keys stored everywhere except in certain countries, and some may want to mix and match rules and say “store them in X and Y, but not in Z”. What we learned from our customers is that they need flexibility, something that will allow them to keep up with the ever-changing rules and policies — and that’s what we set out to build out.

The next issue we faced was scalability.  When we built the initial regions, we included a hard-coded list of data centers that met our criteria for the US, EU, “high security” data center regions.  However, this list was static because the underlying cryptography did not support dynamic changes to our list of data centers. In order to distribute private keys to new data centers that met our criteria, we would have had to completely overhaul the system. In addition to that, our network significantly expands every year, with more than 100 new data centers since the initial launch. That means that any new potential locations that could be used to store private keys are currently not in use, degrading the performance and reliability of customers using this feature.

With our current scale, automation and expansion is a must-have. Our new system needs to dynamically scale every time we onboard or remove a data center from our Network, without any human intervention or large overhaul.

Finally, one of our biggest learnings was that customers make mistakes, such as defining a region that’s so small that availability becomes a concern. Our job is to prevent our customers from making changes that we know will negatively impact them.

Define your own geo-restrictions with the new version of Geo Key Manager

A new, configurable and scalable version of Geo Key Manager, now available in Closed Beta

Cloudflare has significantly grown in the last few years and so has our international customer base. Customers need to keep their traffic regionalized. This region can be as broad as a continent — Asia, for example. Or, it can be a specific country, like Japan.

From our conversations with our customers, we’ve heard that they want to be able to define these regions themselves. This is why today we’re excited to announce that customers will be able to use Geo Key Manager to create what we call “policies”.

A policy can be a single country, defined by two-letter (ISO 3166) country code. It can be a region, such as “EU” for the European Union or Oceania. It can be a mix and match of the two, “country:US or region: EU”.

Our new policy based Geo Key Manager allows you to create allowlist or blocklists of countries and supported regions, giving you control over the boundary in which your private key will be stored. If you’d like to store your private keys globally and omit a few countries, you can do that.

If you would like to store your private keys in the EU and US, you would make the following API call:

curl -X POST "https://api.cloudflare.com/client/v4/zones/zone_id/custom_certificates" \
     -H "X-Auth-Email: [email protected]" \
     -H "X-Auth-Key: auth-key" \
     -H "Content-Type: application/json" \
     --data '{"certificate":"certificate","private_key":"private_key","policy":"(country: US) or (region: EU)", "type": "sni_custom"}'

If you would like to store your private keys in the EU, but not in France, here is how you can define that:

curl -X POST "https://api.cloudflare.com/client/v4/zones/zone_id/custom_certificates" \
     -H "X-Auth-Email: [email protected]" \
     -H "X-Auth-Key: auth-key" \
     -H "Content-Type: application/json" \
     --data '{"certificate":"certificate","private_key":"private_key","policy": "region: EU and (not country: FR)", "type": "sni_custom"}'

Geo Key Manager can now support more than 30 countries and regions. But that’s not all! The superpower of our Geo Key Manager technology is that it doesn’t actually have to be “geo” based, but instead, it’s attribute based. In the future, we’ll have a policy that will allow our customers to define where their private keys are stored based on a compliance standard like FedRAMP or ISO 27001.

Reliability, resiliency, and redundancy

By giving our customers the remote control for Geo Key Manager, we want to make sure that customers understand the impact of their changes on both redundancy and latency.

On the redundancy side, one of our biggest concerns is allowing customers to choose a region small enough that if a data center is removed for maintenance, for example, then availability is drastically impacted. To protect our customers, we’ve added redundancy restrictions. These prevent our customers from setting regions with too few data centers, ensuring that all the data centers within a policy can offer high availability and redundancy.

Not just that, but in the last few years, we’ve significantly improved the underlying networking that powers Geo Key Manager. For more information on how we did that, keep an eye out for a technical deep dive inside Geo Key Manager.

Performance matters

A new, configurable and scalable version of Geo Key Manager, now available in Closed Beta

With the original regions (US, EU, and Highest Security Data Centers), we learned customers may overlook possible latency impacts that occur when defining the key manager to a certain region. Imagine your keys are stored in the US. For your Asia-based customers, there’s going to be some latency impact for the requests that go around the world. Now, with customers being able to define more granular regions, we want to make sure that before customers make that change, they see the impact of it.

If you’re an E-Commerce platform then performance is always top-of-mind. One thing that we’re working on right now is performance metrics for Geo Key Manager policies both from a regional point of view — “what’s the latency impact for Asia based customers?” and from a global point of view — “for anyone in the world, what is the average impact of this policy?”.

By seeing the latency impact, if you see that the impact is unacceptable, you may want to create a separate domain for your service that’s specific to the region that it’s serving.

Closed Beta, now available!

Interested in trying out the latest version of Geo Key Manager? Fill out this form.

Coming soon!

Geo Key Manager is only available via API at the moment. But, we are working on creating an easy-to-use UI for it, so that customers can easily manage their policies and regions. In addition, we’ll surface performance measurements and warnings when we see any degraded impact in terms of performance or redundancy to ensure that customers are mindful when setting policies.

We’re also excited to extend our Geo Key Manager product beyond custom uploaded certificates. In the future, certificates issued through Advanced Certificate Manager or SSL for SaaS will be allowed to add policy based restrictions for the key storage.

Finally, we’re looking to add more default regions to make the selection process simple for our customers. If you have any regions that you’d like us to support, or just general feedback or feature requests related to Geo Key Manager, make a note of it on the form. We love hearing from our customers!

Bringing authentication and identification to Workers through Mutual TLS

Post Syndicated from Dina Kozlov original https://blog.cloudflare.com/mutual-tls-for-workers/

Bringing authentication and identification to Workers through Mutual TLS

Bringing authentication and identification to Workers through Mutual TLS

We’re excited to announce that Workers will soon be able to send outbound requests through a mutually authenticated channel via mutual TLS authentication!

When making outbound requests from a Worker, TLS is always used on the server side, so that the client can validate that the information is being sent to the right destination. But in the same way, the server may want to authenticate the client to ensure that the request is coming from an authorized client. This two-way street of authentication is called Mutual TLS. In this blog, we’re going to talk through the importance of mutual TLS authentication, what it means to use mutual TLS within Workers, and how in a few months you’ll be able to use it to send information through an authenticated channel — adding a layer of security to your application!

mTLS between Cloudflare and an Origin

Mutual TLS authentication works by having a server validate the client certificate against a CA. If the validation passes then the server knows that it’s the right client and will let the request go through. If the validation fails or if a client certificate is not presented then the server can choose to drop the request.

Today, customers use mTLS to secure connections between Cloudflare and an origin — this is done through a product called Authenticated Origin Pull. Once a customer enables it, Cloudflare starts serving a client certificate on all outgoing requests. This is either a Cloudflare managed client certificate or it can be one uploaded by the customer. When enabled, Cloudflare will present this certificate when connecting to an origin. The origin should then check the client certificate to see if it’s the one that it expects to see. If it is then the request will go through. If it’s the wrong client certificate or is not included then the origin can choose to drop the request.

Doing this brings a big security boost because it allows the origin to only accept traffic from Cloudflare and drop any unexpected external traffic.

Digging up problems with dogfooding

Today, many Cloudflare services are built on Cloudflare Workers — it’s the secret sauce we use to continuously ship fast, reliable products to our customers. Internally, we might have one Cloudflare account that runs multiple services, with each service deployed on an individual Worker.

Whenever one service needs to talk to another, the fetch() function is used to request or send information. This can be object data that we send to upstream providers, it can be a read or write to a database, or service to service communication. In most regards, the information that’s going to the origin is sensitive and requires a layer of authentication. Without proper authentication, any client would be able to access the data, removing a layer of security.

Implementing service to service authentication

Today, there are a few ways that you can set up service to service authentication, if you’re building on Workers.

One way to set up service authentication is to use Authenticated Origin Pull. Authenticated Origin Pull allows customers to implement mutual TLS between Cloudflare and an origin by attaching a client certificate and private key to a domain or hostname, so that all outbound requests include a client certificate. The origin can then check this certificate to see whether the request came from Cloudflare. If there’s a valid certificate, then the origin can let the request through and if there’s an invalid certificate or no certificate then the origin can choose to drop the request. However, Authenticated Origin Pull has its limitations and isn’t ideal for some use-cases.

The first limitation is that an Authenticated Origin Pull certificate is tied to a publicly hosted hostname or domain. Some services that are built on Workers don’t necessarily need to be exposed to the public Internet. Therefore, tying it to a domain doesn’t really make sense.

The next limitation is that if you have multiple Workers services that are each writing to the same database, you may want to be able to distinguish them. What if at some point, you need to take the “write” power away from the Worker? Or, what if only Workers A and B are allowed to make writes but Worker C should only make “read” requests?

Today, if you use Authenticated Origin Pulls with Cloudflare’s client certificate then all requests will be accepted as valid. This is because for all outbound requests, we attach the same client certificate. So even though you’re restricting your traffic to “Cloudflare-Only”, there’s no Worker-level granularity.

Now, there’s another solution that you can use. You can make use of Access and set up Token Authentication by using a pre-shared key and configuring your Worker to allow or deny access based on the pre-shared key, presented in the header. While this does allow you to lock down authentication on a per-Worker or per-service basis, the feedback that we’ve gotten from our internal teams who have implemented this is that it’s 1) cumbersome to manage and 2) requires the two service to speak over HTTP, and 3) doesn’t expose the client’s identity. And so, with these limitations in mind, we’re excited to bring mutual TLS authentication to Workers — an easy, scalable way to manage authentication and identity for anyone building on Workers.

Coming soon: Mutual TLS for Workers

We’re excited to announce that in the next few months, we’re going to be bringing mutual TLS support to Workers. Customers will be able to upload client certificates to Cloudflare and attach them in the fetch() requests within a Worker. That way, you can have per-Worker or even per-request level of granularity when it comes to authentication and identification.

When sending out the subrequest, Cloudflare will present the client certificate and the receiving server will be able to check:

1) Is this client presenting a valid certificate?
2) Within Cloudflare, what service or Worker is this request coming from?

This is one of our most highly requested features, both from customers and from internal teams, and we’re excited to launch it and make it a no-brainer for any developer to use Cloudflare as their platform for anything they want to build!